Derivative of Inverse Trigonometric Functions

The derivative of an inverse trigonometric function refers to how fast the value of that inverse trig function changes with respect to the independent variable. Since differentiation measures the rate of change, the derivatives of inverse trigonometric functions help us understand how these functions behave and vary.

Domain of Inverse Trigonometric Functions

We know that a function is differentiable only if it is continuous at that point, and if a function is continuous at a given point, then that point is in the domain of the function. Hence, we should learn the domain of the inverse trigonometric functions for the same.

Inverse Trigonometric Functions	Domain
sin-1x	[-1, 1]
cos-1x	[-1, 1]
tan-1x	R
cosec-1x	(-∞, -1]∪[1, ∞)
sec-1x	(-∞, -1]∪[1, ∞)
cot-1x	R

Implicit Differentiation

Implicit differentiation is a method that uses the chain rule to differentiate implicitly defined functions. An implicit functions is the function which contains two variable rather than one variable. In such case sometimes we can convert the function into one variable explicitly but this not the case always. Since, it is generally not easy to find the function explicitly and then differentiate. Instead, we can totally differentiate f(x, y) i.e. both the variables and then solve the rest of the equation to find the value of f'(x).

These are sin^-1x, cos^-1x, tan^-1x, cosec^-1x, sec^-1x, cot^-1x. We can find the derivative of inverse trigonometric functions using the implicit differentiation method. Let's learn first what are the derivatives of inverse trigonometric functions.

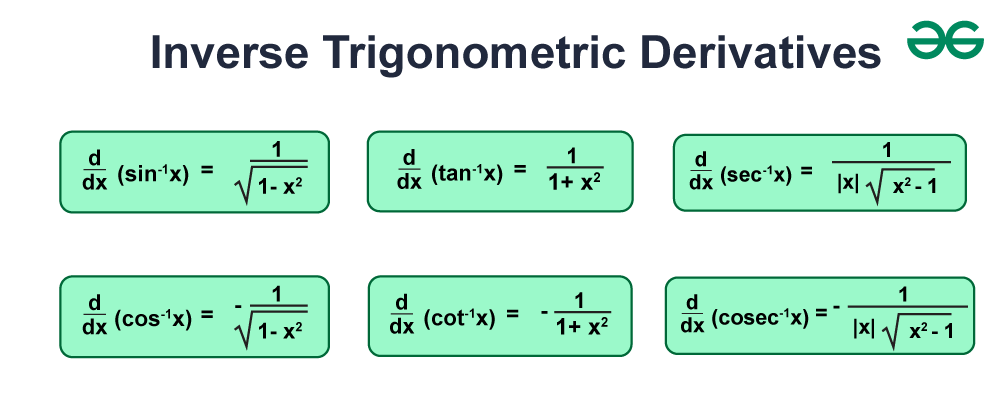
• Derivative of sin^-1x is d(sin^-1x)/dx = 1/√(1 - x²) for all x ϵ (-1, 1)
• Derivative of cos^-1x is d(cos^-1x)/dx = -1/√(1 - x²) for all x ϵ (-1, 1)
• Derivative of tan^-1x is d(tan^-1x)/dx = 1/(1 + x²) for all x ϵ R
• Derivative of cosec^-1x is d(cosec^-1x)/dx = -1/{|x|√(x² - 1)} for all x ϵ R - [-1, 1]
• Derivative of sec^-1x is d(sec^-1x)/dx = 1/{|x|√(x² - 1)} for all x ϵ R - [-1, 1]
• Derivative of cot^-1x is d(cot^-1x)/dx = -1/(1 + x²) for all x ϵ R

Proof of Derivative of Inverse Trigonometric Functions

We can differentiate the inverse trigonometric functions using the first principle and also by using implicit differentiation formula which also involves the use of chain rule. To find the derivative of inverse trigonometric functions using first principle is a lengthy process. In this article we learn how to differentiate inverse trigonometric functions using implicit differentiation. We can find the derivative (dy/dx) of Inverse Trigonometric Functions using following steps.

Step 1: Assume the trigonometric functions in the form sin y = x

Step 2: Find the derivative of above function using implicit differentiation

Step 3: Calculate dy/dx

Step 4: Replace the value of trigonometric function present in the step 3 using trigonometric identities.

Derivative of sin inverse x

Let us assume sin y = x
Differentiating both side with respect to x

⇒ cos y. dy/dx = 1
⇒ dy/dx = 1/cos y →(i)

Since we know that Sin²y + Cos²y = 1

⇒ Cos²y = 1 - sin²y
⇒ cosy = √(1 - sin²y) = √(1 - x²) as we have sin y = x

Putting this value of cos y in equation (i)

dy/dx = 1/√(1 - x²) where y = sin^-1x

Derivative of cos inverse x

Let us assume cos y = x

Differentiating both side with respect to x
⇒ -sin y. dy/dx = 1
⇒ dy/dx = -1/sin y →(i)

Since we know that Sin²y + Cos²y = 1
⇒ sin²y = 1 - cos²y
⇒ sin y = √(1 - cos²y) = √(1 - x²) as we have cos y = x

Putting this value of sin y in equation (i)
dy/dx = -1/√(1 - x²) where y = cos^-1x

Derivative of tan inverse x

Let us assume tan y = x

Differentiating both side with respect to x
⇒ sec²y. dy/dx = 1
⇒ dy/dx = 1/sec²y →(i)

Since we know that sec²y - tan²y = 1
⇒ sec²y = 1 + tan²y
⇒ sec²y = (1 + tan²y) = (1 + x²) as we have tan y = x

Putting this value of sec²y in equation (i)
dy/dx = 1/(1 + x²) where y = tan^-1x

Derivative of cot inverse x

Let us assume cot y = x

Differentiating both side with respect to x
⇒ -cosec² y. dy/dx = 1
⇒ dy/dx = -1/cosec²y →(i)

Since we know that cosec²y - cot²y = 1
⇒ cosec²y = 1 + cot²y
⇒ cosec²y = (1 + cot²y) = (1 + x²) as we have cot y = x

Putting this value of cosec²y in equation (i)
dy/dx = -1/(1 + x²) where y = cot^-1x

Derivative of sec inverse x

Let us assume sec y = x
Differentiating both side with respect to x

⇒ sec y.tan y.dy/dx = 1
⇒ dy/dx = 1/sec y.tan y →(i)

Since we know that sec²y - tan²y = 1

⇒ tan²y = sec²y - 1
⇒ tan y = √(sec²y - 1) = √(x² - 1)as we have sec y = x

Putting this value of tan y in equation (i)

dy/dx = 1/{|x|√(x² - 1)} where sec y = x and y = sec^-1x

Derivative of cosec inverse x

Let us assume cosec y = x
Differentiating both side with respect to x

⇒ -cosec y.cot y.dy/dx = 1
⇒ dy/dx = -1/cosec y.cot y →(i)

Since we know that cosec²y - cot²y = 1

⇒ cot²y = cosec²y - 1
⇒ cot y = √(cosec²y - 1) = √(x² - 1)as we have cosec y = x

Putting this value of tan y in equation (i)
dy/dx = -1/{|x|√(x² - 1)} where cosec y = x and y = cosec^-1x

Inverse Trig Derivative Examples

Example 1: Differentiate sin^-1 (x)?

Solution:

Let, y = sin⁻¹ (x)
Taking sine on both sides of equation gives,
sin y = sin(sin^-1x)

By the property of inverse trigonometry we know, sin(sin^-1x) = x
sin y = x

Now differentiating both sides wrt to x,
d/dx{sin y} = d/dx{x}
{cos y}.dy/dx = 1
dy/dx = 1/ {cos y}

We can simplify it more by using the below observation:

sin²y + cos²y = 1
x² + cos²y = 1 {As sin y = x}
cos²y = 1-x²
cos y = √(1 - x²)

Substituting the value, we get

dy/dx = 1/{cos y}
⇒ dy/dx = 1/√(1 - x²)

Example 2: Differentiate cos^-1 (x)?

Solution:

Let, y = cos⁻¹ (x)

Taking cosine on both sides of equation gives,
cos y = cos(cos^-1x)

By the property of inverse trigonometry we know, cos(cos^-1x) = x
cos (y) = x

Now differentiating both sides wrt to x,
d/dx{cos y} = d/dx{x}
{-sin y}.dy/dx = 1
dy/dx = -1/sin y

We can simplify it more by using the below observation:

sin²y + cos²y = 1
sin²y + x² = 1 {As cos y = x}
sin²y = 1-x²
sin y = √(1 - x²)

Substituting the value, we get
dy/dx = -1/{sin y}
⇒ dy/dx = -1/√(1 - x²)

Example 3: Differentiate tan^-1 (x)?

Solution:

Let, y = tan⁻¹ (x)

Taking tan on both sides of equation gives,
tan y = tan(tan^-1x)

By the property of inverse trigonometry we know, tan(tan^-1x) = x
tan y = x

Now differentiating both sides wrt to x,

d/dx{tan y} = d/dx{x}
sec²(y).dy/dx= 1
dy/dx = 1/sec²y

We can simplify it more by using the below observation:

sec²y = 1 + tan²y
sec²y = 1 + x²

Substituting the value, we get

(1 + x²)dy/dx = 1
dy/dx = 1/(1 + x²)

Example 4: y = cos^-1 (-2x²). Find dy/dx at x = 1/2?

Method 1 (Using implicit differentiation)

Given, y = cos⁻¹ (−2x²)
⇒ cos y = −2x²

Differentiating both sides wrt x
d/dx{cos y} = d/dx{-2x²}
{-sin y}.dy/dx = -4x
dy/dx = 4x/sin y

Simplifying
sin²y + cos²y = 1
sin²y + (-2x²)² = 1 {As cos y = -2x²}
sin²y + 4x⁴ = 1
sin²y = 1 - 4x⁴
sin y = √(1 - 4x⁴)

Putting the obtained value we get,

dy/dx = 4x/√{1 - 4x⁴}
⇒ dy/dx = 4(1/2)/√{1 - 4(1/2)⁴}
⇒ dy/dx = 2/√{1 - 1/4}
⇒ dy/dx = 2/√{3/4}
⇒ dy/dx = 4/√3

Method 2 (Using chain rule as we know the differentiation of cos inverse x)

Given, y = cos⁻¹ (−2x²)

Differentiating both sides wrt x

\begin{aligned} \frac{dy}{dx} &=\frac{d}{dx}  cos^{-1}(-2x^2) \\ &=\frac{-1}{\sqrt{1-(-2x^2)^2}}\ .\ (-4x) \\ &=\frac{4x}{\sqrt{1-4x^4}} \\ &=\frac{4(\frac{1}{2})}{\sqrt{1-4(\frac{1}{2})^4}} \\ &=\frac{2}{\sqrt{1-\frac{1}{4}}} \\ &=\frac{4}{\sqrt{3}} \end{aligned}  

Example 5: Differentiate \begin{aligned}sin^{-1}(\frac{1-x}{1+x}) \end{aligned}

Solutions:

Let, \begin{aligned} y = sin^{-1}(\frac{1-x}{1+x}) \end{aligned}

Differentiating both sides wrt x

\begin{aligned} \frac{dy}{dx} &= \frac{d}{dx}sin^{-1}(\frac{1-x}{1+x}) \\ &= \frac{1}{\sqrt{1-(\frac{1-x}{1+x})^2}} \ . \frac{d}{dx}(\frac{1-x}{1+x}) \\ &= \frac{1+x}{\sqrt{(1+x)^2-({1-x})^2}} \ . \frac{-(1+x)-(1-x)}{(1+x)^2} \\ &= \frac{1}{\sqrt{(1+x)^2-({1-x})^2}} \ . \frac{-2}{(1+x)} \\ &= \frac{1}{\sqrt{4x}} \ . \frac{-2}{(1+x)} \\ &= \frac{-1}{\sqrt{x}(1+x)} \\ \end{aligned}

Inverse Trigonometric Function Derivative Questions

Q1: Differentiate sin^-1(3x - 4x³) for x ϵ -1/2 < x < 1/2

Q2: Differentiate cos^-1(2x² - 1) for 0 < x < 1

Q3: Differentiate tan^-1(2x/1 - x²) for x ϵ (-1, 1)

Q4: Differentiate sin^-1(2x/1 + x²) for x ϵ (-1, 1)