Zero-Sum Game
Last Updated :
26 Feb, 2021
Zero-Sum Game:
A zero-sum game is one in which no wealth is created or destroyed. So, in a two-player zero-sum game, whatever one player wins, the other loses. In this game, we can include at least two and a maximum to an infinite number of contestants. It assumes a version of perfect competition and perfect information.
Let us consider a game in which n contestant takes part, and contestant i has Ni courses of action available to him. Then the number of outcomes to a play of the game will be N1, N2,……………, Nn. So, consider a possible outcome θ result in payment p(i, θ) to a contestant i. Then, the game is called a Zero-Sum Game, if every possible result θ, we have
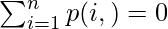
Lets us understand this by taking an example, three-man A, B, and C playing poker and put 100 bucks all, the winner takes all money. If A wins the game he gains 200 bucks but B and C lose 100 bucks each. So, the total payment to all contestants after the play is zero. Similarly, if B or C wins too.
In financial markets, futures and options are considered non-zero games because contracts represent agreements between two parties and, if one investor loses, the asset is transferred to another investor. Poker, Gambling, Matching Pennies, Chess, Tennis are also some examples of Zero-Sum Game.
Share your thoughts in the comments
Please Login to comment...