Work Done by a Variable Force

Usually, a dancing person is considered to be more energetic compared to a sitting person. A security guard who has been standing at his place the whole day has been working for hours. In real life, this seems obvious, but these terms and definitions work differently when it comes to physics. In physics, work has been defined as the product of force and displacement. This means, that if there is no displacement, work done is zero, no matter how much force or time was spent. This definition builds up concepts like the work-energy theorem. Let’s see this in detail. 

Work 

Consider a block of mass M sitting on a surface. Now, Aman comes and starts applying a force F, on the block. Only applying the force for some time, he is able to shift the block by 4 meters on the surface. The block and the force are shown in the figure below. Now, since displacement is there. According to physics terminology, the work is done. 

For a constant force and the displacement 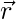. The work done is defined by, 

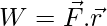
This is the dot product between two vectors, so if the Force makes an angle 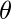 with the displacement. Then the work done will be given by, 

W = |F||r|cos()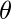

Work done by a Variable Force

The above equations are cases of calculating work done with the assumption that the force that is being applied to the body is constant. Often, this is not the case. Forces vary in direction and magnitude with time and sometimes with distance too. So, calculating the work done with this assumption is not right and is not perfectly generalizable. 

Let’s consider a force that changes its magnitude. Consider the case of a spring and Hooke’s law. According to Hooke’s law, the restoring force of a perfectly elastic spring is proportional to its extension. The direction of this force is opposite to the extension. There the force acting is given by, 

F = -kx

Here, k is the spring constant. 

This is an example of a variable Force. For calculating the work done by a variable force, we should add all the infinitely small work done in all the infinitesimally small intervals. Let’s denote the infinitesimally small interval by “dt”. So, to add to the work done in such a scenario, an integral must be used. 

The interval “dt” can be used to calculate the change in the extension of spring. 

dx = vdt

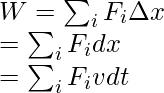
Using the relations of force from the Hooke’s law. 

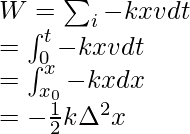
This work is done by a force applied on the spring for an extension of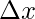 

For a force which is varying and is given by 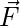and produces a displacement given by the vector 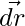. The work done is given by, 

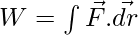
Force-Displacement Plot

The above concept can be understood more clearly using the force-displacement plot. The plot below shows a variable force with the displacement it is producing. It is known that the integrals represent the area under the curve. So, in this case, the area under the curve gives the work done by the force on the body. The area under the curve is divided into many rectangles which represent the 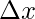 displacement. 

The area of a single rectangle is 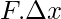. This represents the work done by the force for an infinitesimally small displacement. The total sum of the area of all the rectangles gives the total work done. 

W =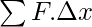 

⇒ W = ∫Fdx

Sample Problems

Question 1: Find the work done when a force of 20N acting in the direction of displacement produces a displacement of 5 m. 

Solution: 

The work done by a constant force is given by, 

W = |F||r|cos()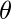

Here, 

W = |F||r|cos()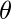

⇒ W = (20)(5)(cos(0)) 

⇒ W= 100

Question 2: Find the work done when a force of F = 30i + 5j produces a displacement r = 5i + 2j. 

Solution: 

The work done by a constant force is given by, 

W =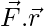 

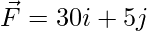 and 

Calculating the dot product. 

W =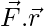 

⇒ W = (30i + 5j). (5i + 2j) 

⇒ W= (30)(5) + (5)(2) 

⇒W = 150 + 10 

⇒W = 160 J

Question 3: Find the work done when a force of F = x produces a displacement of 4m. 

Solution: 

The work done by a variable force is given by, 

W = ∫Fdx

F(x) = x

Calculating the work done.

W = 

Here, the displacement is x = 4 

W =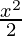 

⇒ W =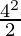 

⇒ W = 8J

Question 4: Find the work done when a force of F = x² produces a displacement of 3 m. 

Solution: 

The work done by a variable force is given by, 

W = ∫Fdx

F(x) = x²

Calculating the work done. 

W = 

Here, the displacement is x = 3 

W =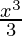 

⇒ W = 

⇒ W = 27/3 ⇒ 9J

Question 5: Find the work done when a force of F = x + 4 produces a displacement of 2 m. 

Solution: 

The work done by a variable force is given by, 

W = ∫Fdx

F(x) = x + 4

Calculating the work done. 

W = 

Here, the displacement is x = 2

W =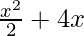 

⇒ W =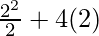 

⇒ W = 10 J

Question 6: Find the work done when a force of F = sin(x) produces a displacement from -1 to 1. 

Solution: 

The work done by a variable force is given by, 

W = ∫Fdx

F(x) = sin(x)

Calculating the work done. 

W = 

FAQs on Work Done by a Variable Force

What is work done by variable force?

Work done by a variable force is the product of the force and the displacement of an object in the direction of the force when the force acting on the object varies with position or time.

What is a variable force?

A force is considered variable if its magnitude and/or direction changes with respect to the position, time, or other parameters of the system. Examples of variable forces include gravitational force, magnetic force, etc.

Is friction a variable force?

Friction is often considered a variable force because its magnitude depends on various factors such as the nature of the surfaces in contact, the normal force between the surfaces, and the relative motion or tendency for motion between the surfaces

Why is spring force a variable force?

The force exerted by a spring (also known as the spring force or restoring force) is considered variable because it varies with the displacement of the spring from its equilibrium position.

How to calculate work with a variable force?

To calculate the work done by a variable force,we use the following formula: