Word Break Problem | DP-32

Given an input string and a dictionary of words, find out if the input string can be segmented into a space-separated sequence of dictionary words. See following examples for more details. 
This is a famous Google interview question, also being asked by many other companies now a days.

Consider the following dictionary 
{ i, like, sam, sung, samsung, mobile, ice, 
  cream, icecream, man, go, mango}
Input:  ilike
Output: Yes 
The string can be segmented as "i like".
Input:  ilikesamsung
Output: Yes
The string can be segmented as "i like samsung" 
or "i like sam sung".

Recursive implementation:
The idea is simple, we consider each prefix and search for it in dictionary. If the prefix is present in dictionary, we recur for rest of the string (or suffix).

C++

#include <algorithm>
#include <iostream>
#include <string>
#include <vector>

using namespace std;

// Function to check if the given word can be broken
// down into words from the wordList
bool WordBreak(const vector<string>& wordList,
               const string& word)
{
    // If the word is empty, it can be broken down into
    // an empty list of words
    if (word.empty())
        return true;

    int wordLen = word.length();

    // Check if the word can be broken down into
    // words from the wordList
    for (int i = 1; i <= wordLen; ++i) {
        string prefix = word.substr(0, i);

        if (find(wordList.begin(), wordList.end(), prefix)
                != wordList.end()
            && WordBreak(wordList, word.substr(i))) {
            return true;
        }
    }

    return false;
}

int main()
{
    vector<string> wordList
        = { "mobile", "samsung",  "sam",  "sung", "man",
            "mango",  "icecream", "and",  "go",   "i",
            "like",   "ice",      "cream" };

    bool result = WordBreak(wordList, "ilikesamsung");

    cout << boolalpha << result << endl; // Output: true

    return 0;
}

Java

import java.util.*;

public class Main {
    // Function to check if the given word can be broken
    // down into words from the wordList
    static boolean wordBreak(List<String> wordList,
                             String word)
    {
        // If the word is empty, it can be broken down into
        // an empty list of words
        if (word.isEmpty()) {
            return true;
        }

        int wordLen = word.length();

        // Check if the word can be broken down into
        // words from the wordList
        for (int i = 1; i <= wordLen; ++i) {
            String prefix = word.substring(0, i);

            if (wordList.contains(prefix)
                && wordBreak(wordList, word.substring(i))) {
                return true;
            }
        }

        return false;
    }

    public static void main(String[] args)
    {
        List<String> wordList = Arrays.asList(
            "mobile", "samsung", "sam", "sung", "man",
            "mango", "icecream", "and", "go", "i", "like",
            "ice", "cream");

        boolean result
            = wordBreak(wordList, "ilikesamsung");

        System.out.println(result); // Output: true
    }
}

Python3

def wordBreak(wordList, word):
    if word == '':
        return True
    else:
        wordLen = len(word)
        return any([(word[:i] in wordList) and wordBreak(wordList, word[i:]) for i in range(1, wordLen+1)])

C#

using System;
using System.Collections.Generic;
using System.Linq;

class GFG {
    // Function to check if the given word can be broken
    // down into words from the wordList
    public static bool WordBreak(List<string> wordList,
                                 string word)
    {
        // If the word is empty, it can be broken down into
        // an empty list of words
        if (word == "")
            return true;

        int wordLen = word.Length;

        // Check if the word can be broken down into
        // words from the wordList
        return Enumerable.Range(1, wordLen)
            .Any(i
                 => wordList.Contains(word.Substring(0, i))
                   && WordBreak(wordList,
                                word.Substring(i)));
    }

    public static void Main(string[] args)
    {

        Console.WriteLine(WordBreak(
            new List<string>(new string[] {
                "mobile", "samsung", "sam", "sung", "man",
                "mango", "icecream", "and", "go", "i",
                "like", "ice", "cream" }),
            "ilikesamsung"));
    }
}

Javascript

// Function to check if the given word can be broken down into words from the wordList
function wordBreak(wordList, word) {
    // If the word is empty, it can be broken down into an empty list of words
    if (word === '') {
        return true;
    }

    const wordLen = word.length;

    // Check if the word can be broken down into words from the wordList
    for (let i = 1; i <= wordLen; i++) {
        const prefix = word.substr(0, i);

        if (wordList.includes(prefix) && wordBreak(wordList, word.substr(i))) {
            return true;
        }
    }

    return false;
}

// Main function
function main() {
    const wordList = [
        "mobile", "samsung", "sam", "sung", "man",
        "mango", "icecream", "and", "go", "i",
        "like", "ice", "cream"
    ];

    const result = wordBreak(wordList, "ilikesamsung");

    console.log(result); // Output: true
}

// Call the main function
main();

Output

true

If the recursive call for suffix returns true, we return true, otherwise we try next prefix. If we have tried all prefixes and none of them resulted in a solution, we return false.
We strongly recommend to see substr function which is used extensively in following implementations.

C++

// A recursive program to test whether a given
// string can be segmented into space separated
// words in dictionary
#include <iostream>
using namespace std;

/* A utility function to check whether a word is
  present in dictionary or not. An array of strings
  is used for dictionary.  Using array of strings for
  dictionary is definitely not a good idea. We have
  used for simplicity of the program*/
int dictionaryContains(string word)
{
    string dictionary[] = {"mobile","samsung","sam","sung",
                            "man","mango","icecream","and",
                             "go","i","like","ice","cream"};
    int size = sizeof(dictionary)/sizeof(dictionary[0]);
    for (int i = 0; i < size; i++)
        if (dictionary[i].compare(word) == 0)
           return true;
    return false;
}

// returns true if string can be segmented into space
// separated words, otherwise returns false
bool wordBreak(string str)
{
    int size = str.size();

    // Base case
    if (size == 0)  return true;

    // Try all prefixes of lengths from 1 to size
    for (int i=1; i<=size; i++)
    {
        // The parameter for dictionaryContains is
        // str.substr(0, i) which is prefix (of input
        // string) of length 'i'. We first check whether
        // current prefix is in  dictionary. Then we
        // recursively check for remaining string
        // str.substr(i, size-i) which is suffix of
        // length size-i
        if (dictionaryContains( str.substr(0, i) ) &&
            wordBreak( str.substr(i, size-i) ))
            return true;
    }

    // If we have tried all prefixes and
    // none of them worked
    return false;
}

// Driver program to test above functions
int main()
{
    wordBreak("ilikesamsung")? cout <<"Yes\n": cout << "No\n";
    wordBreak("iiiiiiii")? cout <<"Yes\n": cout << "No\n";
    wordBreak("")? cout <<"Yes\n": cout << "No\n";
    wordBreak("ilikelikeimangoiii")? cout <<"Yes\n": cout << "No\n";
    wordBreak("samsungandmango")? cout <<"Yes\n": cout << "No\n";
    wordBreak("samsungandmangok")? cout <<"Yes\n": cout << "No\n";
    return 0;
}

Java

import java.util.*;

// Recursive implementation of
// word break problem in java
public class WordBreakProblem
{

    // set to hold dictionary values
    private static Set<String> dictionary = new HashSet<>();

    public static void main(String []args)
    {

        // array of strings to be added in dictionary set.
        String temp_dictionary[] = {"mobile","samsung","sam","sung",
                            "man","mango","icecream","and",
                            "go","i","like","ice","cream"};

        // loop to add all strings in dictionary set
        for (String temp :temp_dictionary)
        {
            dictionary.add(temp);
        }

        // sample input cases
        System.out.println(wordBreak("ilikesamsung"));
        System.out.println(wordBreak("iiiiiiii"));
        System.out.println(wordBreak(""));
        System.out.println(wordBreak("ilikelikeimangoiii"));
        System.out.println(wordBreak("samsungandmango"));
        System.out.println(wordBreak("samsungandmangok"));

    }

    // returns true if the word can be segmented into parts such
    // that each part is contained in dictionary
    public static boolean wordBreak(String word)
    {
        int size = word.length();

        // base case
        if (size == 0)
        return true;

        //else check for all words
        for (int i = 1; i <= size; i++)
        {
            // Now we will first divide the word into two parts ,
            // the prefix will have a length of i and check if it is
            // present in dictionary ,if yes then we will check for
            // suffix of length size-i recursively. if both prefix and
            // suffix are present the word is found in dictionary.

            if (dictionary.contains(word.substring(0,i)) &&
                    wordBreak(word.substring(i,size)))
            return true;
        }

        // if all cases failed then return false
        return false;
    }
}

// This code is contributed by Sparsh Singhal

Python3

# Recursive implementation of
# word break problem in Python

# returns True if the word can be segmented into parts such
# that each part is contained in dictionary
def wordBreak(word):

    global dictionary

    size = len(word)

    # base case
    if (size == 0):
        return True

    # else check for all words
    for i in range(1,size + 1):
        # Now we will first divide the word into two parts ,
        # the prefix will have a length of i and check if it is
        # present in dictionary ,if yes then we will check for
        # suffix of length size-i recursively. if both prefix and
        # suffix are present the word is found in dictionary.

        if (word[0:i] in dictionary and wordBreak(word[i: size])):
            return True

    # if all cases failed then return False
    return False

# set to hold dictionary values
dictionary = set()

# array of strings to be added in dictionary set.
temp_dictionary = [ "mobile", "samsung", "sam", "sung", "man", "mango", "icecream", "and", "go", "i","like", "ice", "cream" ]

# loop to add all strings in dictionary set
for temp in temp_dictionary:
    dictionary.add(temp)

# sample input cases
print("Yes" if wordBreak("ilikesamsung") else "No")
print("Yes" if wordBreak("iiiiiiii") else "No")
print("Yes" if wordBreak("") else "No")
print("Yes" if wordBreak("ilikelikeimangoiii") else "No")
print("Yes" if wordBreak("samsungandmango") else "No")
print("Yes" if wordBreak("samsungandmangok") else "No")

# This code is contributed by shinjanpatra

C#

using System;
using System.Collections.Generic;

// Recursive implementation of word break problem in C#
public class WordBreakProblem
{
    // HashSet to hold dictionary values
    private static HashSet<string> dictionary = new HashSet<string>();


    // Returns true if the word can be segmented into parts such
    // that each part is contained in dictionary
    public static bool wordBreak(string word)
    {
        int size = word.Length;

        // Base case
        if (size == 0)
            return true;

        // Else check for all words
        for (int i = 1; i <= size; i++)
        {
            // Divide the word into two parts, the prefix will have a length of i
            // and check if it is present in dictionary, if yes then we will check
            // for suffix of length size-i recursively. If both prefix and
            // suffix are present the word is found in dictionary.
            if (dictionary.Contains(word.Substring(0, i)) &&
                wordBreak(word.Substring(i, size - i)))
                return true;
        }

        // If all cases failed then return false
        return false;
    }
  static void Main(string[] args)
    {
        // Array of strings to be added in dictionary HashSet
        string[] temp_dictionary = { "mobile", "samsung", "sam", "sung",
                            "man", "mango", "icecream", "and",
                            "go", "i", "like", "ice", "cream" };

        // Loop to add all strings in dictionary HashSet
        foreach (string temp in temp_dictionary)
        {
            dictionary.Add(temp);
        }

        // Sample input cases
        Console.WriteLine(wordBreak("ilikesamsung"));
        Console.WriteLine(wordBreak("iiiiiiii"));
        Console.WriteLine(wordBreak(""));
        Console.WriteLine(wordBreak("ilikelikeimangoiii"));
        Console.WriteLine(wordBreak("samsungandmango"));
        Console.WriteLine(wordBreak("samsungandmangok"));
    }
}

Javascript

<script>
// Recursive implementation of
// word break problem in java

    // set to hold dictionary values
    var dictionary = new Set();


        // array of strings to be added in dictionary set.
        var temp_dictionary = [ "mobile", "samsung", "sam", "sung", "man", "mango", "icecream", "and", "go", "i",
                "like", "ice", "cream" ];

        // loop to add all strings in dictionary set
        for (var temp of temp_dictionary) {
            dictionary.add(temp);
        }

        // sample input cases
        document.write(((wordBreak("ilikesamsung"))?"Yes":"No")+"<br/>");
        document.write(((wordBreak("iiiiiiii"))?"Yes":"No")+"<br/>");
        document.write(((wordBreak(""))?"Yes":"No")+"<br/>");
        document.write(((wordBreak("ilikelikeimangoiii"))?"Yes":"No")+"<br/>");
        document.write(((wordBreak("samsungandmango"))?"Yes":"No")+"<br/>");
        document.write(((wordBreak("samsungandmangok"))?"Yes":"No")+"<br/>");


    // returns true if the word can be segmented into parts such
    // that each part is contained in dictionary
    function wordBreak( word) {
        var size = word.length;

        // base case
        if (size == 0)
            return true;

        // else check for all words
        for (var i = 1; i <= size; i++) {
            // Now we will first divide the word into two parts ,
            // the prefix will have a length of i and check if it is
            // present in dictionary ,if yes then we will check for
            // suffix of length size-i recursively. if both prefix and
            // suffix are present the word is found in dictionary.

            if (dictionary.has(word.substring(0, i)) && wordBreak(word.substring(i, size)))
                return true;
        }

        // if all cases failed then return false
        return false;
}

// This code is contributed by Rajput-Ji
</script>

Output

Yes
Yes
Yes
Yes
Yes
No

Time Complexity: The time complexity of the above code will be O(2^n).
Auxiliary Space: The space complexity will be O(n) as we are using recursion and the recursive call stack will take O(n) space.

Dynamic Programming
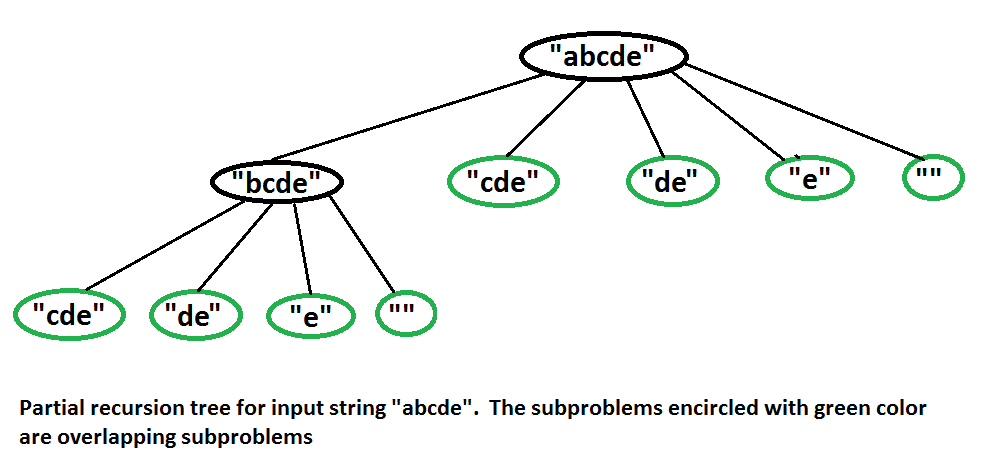
Why Dynamic Programming? The above problem exhibits overlapping sub-problems. For example, see the following partial recursion tree for string “abcde” in the worst case.

CPP

// A Dynamic Programming based program to test whether a given string can
// be segmented into space separated words in dictionary
#include <iostream>
#include <string.h>
using namespace std;

/* A utility function to check whether a word is present in dictionary or not.
  An array of strings is used for dictionary.  Using array of strings for
  dictionary is definitely not a good idea. We have used for simplicity of
  the program*/
int dictionaryContains(string word)
{
    string dictionary[] = {"mobile","samsung","sam","sung","man","mango",
                           "icecream","and","go","i","like","ice","cream"};
    int size = sizeof(dictionary)/sizeof(dictionary[0]);
    for (int i = 0; i < size; i++)
        if (dictionary[i].compare(word) == 0)
           return true;
    return false;
}

// Returns true if string can be segmented into space separated
// words, otherwise returns false
bool wordBreak(string str)
{
    int size = str.size();
    if (size == 0)   return true;

    // Create the DP table to store results of subproblems. The value wb[i]
    // will be true if str[0..i-1] can be segmented into dictionary words,
    // otherwise false.
    bool wb[size+1];
    memset(wb, 0, sizeof(wb)); // Initialize all values as false.

    for (int i=1; i<=size; i++)
    {
        // if wb[i] is false, then check if current prefix can make it true.
        // Current prefix is "str.substr(0, i)"
        if (wb[i] == false && dictionaryContains( str.substr(0, i) ))
            wb[i] = true;

        // wb[i] is true, then check for all substrings starting from
        // (i+1)th character and store their results.
        if (wb[i] == true)
        {
            // If we reached the last prefix
            if (i == size)
                return true;

            for (int j = i+1; j <= size; j++)
            {
                // Update wb[j] if it is false and can be updated
                // Note the parameter passed to dictionaryContains() is
                // substring starting from index 'i' and length 'j-i'
                if (wb[j] == false && dictionaryContains( str.substr(i, j-i) ))
                    wb[j] = true;

                // If we reached the last character
                if (j == size && wb[j] == true)
                    return true;
            }
        }
    }

    /* Uncomment these lines to print DP table "wb[]"
     for (int i = 1; i <= size; i++)
        cout << " " << wb[i]; */

    // If we have tried all prefixes and none of them worked
    return false;
}

// Driver program to test above functions
int main()
{
    wordBreak("ilikesamsung")? cout <<"Yes\n": cout << "No\n";
    wordBreak("iiiiiiii")? cout <<"Yes\n": cout << "No\n";
    wordBreak("")? cout <<"Yes\n": cout << "No\n";
    wordBreak("ilikelikeimangoiii")? cout <<"Yes\n": cout << "No\n";
    wordBreak("samsungandmango")? cout <<"Yes\n": cout << "No\n";
    wordBreak("samsungandmangok")? cout <<"Yes\n": cout << "No\n";
    return 0;
}

Java

// A Dynamic Programming based program to test whether a given String can
// be segmented into space separated words in dictionary
import java.util.*;

class GFG{

/* A utility function to check whether a word is present in dictionary or not.
  An array of Strings is used for dictionary.  Using array of Strings for
  dictionary is definitely not a good idea. We have used for simplicity of
  the program*/
static boolean dictionaryContains(String word)
{
    String dictionary[] = {"mobile","samsung","sam","sung","man","mango",
                           "icecream","and","go","i","like","ice","cream"};
    int size = dictionary.length;
    for (int i = 0; i < size; i++)
        if (dictionary[i].compareTo(word) == 0)
           return true;
    return false;
}

// Returns true if String can be segmented into space separated
// words, otherwise returns false
static boolean wordBreak(String str)
{
    int size = str.length();
    if (size == 0)   return true;

    // Create the DP table to store results of subproblems. The value wb[i]
    // will be true if str[0..i-1] can be segmented into dictionary words,
    // otherwise false.
    boolean []wb = new boolean[size+1];

    for (int i=1; i<=size; i++)
    {
        // if wb[i] is false, then check if current prefix can make it true.
        // Current prefix is "str.substring(0, i)"
        if (wb[i] == false && dictionaryContains( str.substring(0, i) ))
            wb[i] = true;

        // wb[i] is true, then check for all subStrings starting from
        // (i+1)th character and store their results.
        if (wb[i] == true)
        {
            // If we reached the last prefix
            if (i == size)
                return true;

            for (int j = i+1; j <= size; j++)
            {
                // Update wb[j] if it is false and can be updated
                // Note the parameter passed to dictionaryContains() is
                // subString starting from index 'i' and length 'j-i'
                if (wb[j] == false && dictionaryContains( str.substring(i, j) ))
                    wb[j] = true;

                // If we reached the last character
                if (j == size && wb[j] == true)
                    return true;
            }
        }
    }

    /* Uncomment these lines to print DP table "wb[]"
     for (int i = 1; i <= size; i++)
        System.out.print(" " +  wb[i]; */

    // If we have tried all prefixes and none of them worked
    return false;
}

// Driver program to test above functions
public static void main(String[] args)
{
    if(wordBreak("ilikesamsung"))
        System.out.print("Yes\n");
    else
        System.out.print("No\n");
    if(wordBreak("iiiiiiii"))
        System.out.print("Yes\n");
    else
        System.out.print("No\n");
    if(wordBreak(""))
        System.out.print("Yes\n");
    else
        System.out.print("No\n");
    if(wordBreak("ilikelikeimangoiii"))
        System.out.print("Yes\n");
    else
        System.out.print("No\n");
    if(wordBreak("samsungandmango"))
        System.out.print("Yes\n");
    else
        System.out.print("No\n");
    if(wordBreak("samsungandmangok"))
        System.out.print("Yes\n");
    else
        System.out.print("No\n");
   }
}

// This code is contributed by Rajput-Ji

Python3

# A Dynamic Programming based program to test whether a given String can
# be segmented into space separated words in dictionary

# A utility function to check whether a word is present in dictionary or not.
# An array of Strings is used for dictionary. Using array of Strings for
# dictionary is definitely not a good idea. We have used for simplicity of the
# program
def dictionaryContains(word):
    dictionary = [ "mobile", "samsung", "sam", "sung", "man", "mango", "icecream", "and", "go", "i",
                "like", "ice", "cream" ]
    size = len(dictionary)
    for i in range(size):
        if (dictionary[i]== word):
            return True
    return False

# Returns True if String can be segmented into space separated
# words, otherwise returns False
def wordBreak(Str):
    size = len(Str)
    if (size == 0):
        return True

        # Create the DP table to store results of subproblems. The value wb[i]
        # will be True if str[0..i-1] can be segmented into dictionary words,
        # otherwise False.
    wb = [False for i in range(size + 1)]

    for i in range(1,size + 1):
        # if wb[i] is False, then check if current prefix can make it True.
        # Current prefix is "str.substring(0, i)"
        if (wb[i] == False and dictionaryContains(Str[0: i])):
            wb[i] = True

        # wb[i] is True, then check for all subStrings starting from
        # (i+1)th character and store their results.
        if (wb[i] == True):
            # If we reached the last prefix
            if (i == size):
                return True

            for j in range(i + 1,size + 1):
                # Update wb[j] if it is False and can be updated
                # Note the parameter passed to dictionaryContains() is
                # subString starting from index 'i' and length 'j-i'
                if (wb[j] == False and dictionaryContains(Str[i: j])):
                    wb[j] = True

                # If we reached the last character
                if (j == size and wb[j] == True):
                    return True



    # If we have tried all prefixes and none of them worked
    return False

# Driver program to test above functions

if (wordBreak("ilikesamsung")):
    print("Yes")
else:
    print("No")
if (wordBreak("iiiiiiii")):
    print("Yes")
else:
    print("No")
if (wordBreak("")):
    print("Yes")
else:
    print("No")
if (wordBreak("ilikelikeimangoiii")):
    print("Yes")
else:
    print("No")
if (wordBreak("samsungandmango")):
    print("Yes")
else:
    print("No")
if (wordBreak("samsungandmangok")):
    print("Yes")
else:
    print("No")

# This code is contributed by shinjanpatra

C#

// A Dynamic Programming based program to test whether a given String can
// be segmented into space separated words in dictionary

// Include namespace system
using System;

public class GFG
{
    // A utility function to check whether a word is present in dictionary or not.
    //  An array of Strings is used for dictionary.  Using array of Strings for
    //  dictionary is definitely not a good idea. We have used for simplicity of
    //  the program
    public static bool dictionaryContains(String word)
    {
        String[] dictionary = {"mobile", "samsung", "sam", "sung", "man", "mango", "icecream", "and", "go", "i", "like", "ice", "cream"};
        var size = dictionary.Length;
        for (int i = 0; i < size; i++)
        {
            if (string.CompareOrdinal(dictionary[i],word) == 0)
            {
                return true;
            }
        }
        return false;
    }
    // Returns true if String can be segmented into space separated
    // words, otherwise returns false
    public static bool wordBreak(String str)
    {
        var size = str.Length;
        if (size == 0)
        {
            return true;
        }
        // Create the DP table to store results of subproblems. The value wb[i]
        // will be true if str[0..i-1] can be segmented into dictionary words,
        // otherwise false.
        bool[] wb = new bool[size + 1];
        for (int i = 1; i <= size; i++)
        {
            // if wb[i] is false, then check if current prefix can make it true.
            // Current prefix is "str.substring(0, i)"
            if (wb[i] == false && GFG.dictionaryContains(str.Substring(0,i-0)))
            {
                wb[i] = true;
            }
            // wb[i] is true, then check for all subStrings starting from
            // (i+1)th character and store their results.
            if (wb[i] == true)
            {
                // If we reached the last prefix
                if (i == size)
                {
                    return true;
                }
                for (int j = i + 1; j <= size; j++)
                {
                    // Update wb[j] if it is false and can be updated
                    // Note the parameter passed to dictionaryContains() is
                    // subString starting from index 'i' and length 'j-i'
                    if (wb[j] == false && GFG.dictionaryContains(str.Substring(i,j-i)))
                    {
                        wb[j] = true;
                    }
                    // If we reached the last character
                    if (j == size && wb[j] == true)
                    {
                        return true;
                    }
                }
            }
        }
        // Uncomment these lines to print DP table "wb[]"
        //     for (int i = 1; i <= size; i++)
        //        System.out.print(" " +  wb[i];
        // If we have tried all prefixes and none of them worked
        return false;
    }
    // Driver program to test above functions
    public static void Main(String[] args)
    {
        if (GFG.wordBreak("ilikesamsung"))
        {
            Console.Write("Yes\n");
        }
        else
        {
            Console.Write("No\n");
        }
        if (GFG.wordBreak("iiiiiiii"))
        {
            Console.Write("Yes\n");
        }
        else
        {
            Console.Write("No\n");
        }
        if (GFG.wordBreak(""))
        {
            Console.Write("Yes\n");
        }
        else
        {
            Console.Write("No\n");
        }
        if (GFG.wordBreak("ilikelikeimangoiii"))
        {
            Console.Write("Yes\n");
        }
        else
        {
            Console.Write("No\n");
        }
        if (GFG.wordBreak("samsungandmango"))
        {
            Console.Write("Yes\n");
        }
        else
        {
            Console.Write("No\n");
        }
        if (GFG.wordBreak("samsungandmangok"))
        {
            Console.Write("Yes\n");
        }
        else
        {
            Console.Write("No\n");
        }
    }
}

// This code is contributed by mukulsomukesh

Javascript

<script>
// A Dynamic Programming based program to test whether a given String can
// be segmented into space separated words in dictionary

    /*
     * A utility function to check whether a word is present in dictionary or not.
     * An array of Strings is used for dictionary. Using array of Strings for
     * dictionary is definitely not a good idea. We have used for simplicity of the
     * program
     */
    function dictionaryContains( word) {
        var dictionary = [ "mobile", "samsung", "sam", "sung", "man", "mango", "icecream", "and", "go", "i",
                "like", "ice", "cream" ];
        var size = dictionary.length;
        for (var i = 0; i < size; i++)
            if (dictionary[i]===(word))
                return true;
        return false;
    }

    // Returns true if String can be segmented into space separated
    // words, otherwise returns false
    function wordBreak( str) {
        var size = str.length;
        if (size == 0)
            return true;

        // Create the DP table to store results of subproblems. The value wb[i]
        // will be true if str[0..i-1] can be segmented into dictionary words,
        // otherwise false.
        var wb = Array(size + 1).fill(false);

        for (var i = 1; i <= size; i++) {
            // if wb[i] is false, then check if current prefix can make it true.
            // Current prefix is "str.substring(0, i)"
            if (wb[i] == false && dictionaryContains(str.substring(0, i)))
                wb[i] = true;

            // wb[i] is true, then check for all subStrings starting from
            // (i+1)th character and store their results.
            if (wb[i] == true) {
                // If we reached the last prefix
                if (i == size)
                    return true;

                for (j = i + 1; j <= size; j++) {
                    // Update wb[j] if it is false and can be updated
                    // Note the parameter passed to dictionaryContains() is
                    // subString starting from index 'i' and length 'j-i'
                    if (wb[j] == false && dictionaryContains(str.substring(i, j)))
                        wb[j] = true;

                    // If we reached the last character
                    if (j == size && wb[j] == true)
                        return true;
                }
            }
        }

        /*
         * Uncomment these lines to print DP table "wb" for (i = 1; i <= size;
         * i++) document.write(" " + wb[i];
         */

        // If we have tried all prefixes and none of them worked
        return false;
    }

    // Driver program to test above functions

        if (wordBreak("ilikesamsung"))
            document.write("Yes<br/>");
        else
            document.write("No<br/>");
        if (wordBreak("iiiiiiii"))
            document.write("Yes<br/>");
        else
            document.write("No<br/>");
        if (wordBreak(""))
            document.write("Yes<br/>");
        else
            document.write("No<br/>");
        if (wordBreak("ilikelikeimangoiii"))
            document.write("Yes<br/>");
        else
            document.write("No<br/>");
        if (wordBreak("samsungandmango"))
            document.write("Yes<br/>");
        else
            document.write("No<br/>");
        if (wordBreak("samsungandmangok"))
            document.write("Yes<br/>");
        else
            document.write("No<br/>");

// This code contributed by Rajput-Ji
</script>

Output

Yes
Yes
Yes
Yes
Yes
No

The time complexity of the given implementation of the wordBreak function is O(n^3), where n is the length of the input string.

The space complexity of the implementation is O(n), as an extra boolean array of size n+1 is created. Additionally, the dictionary array occupies a space of O(kL), where k is the number of words in the dictionary and L is the maximum length of a word in the dictionary. However, since the dictionary is a constant and small-sized array, its space complexity can be considered negligible. Therefore, the overall space complexity of the implementation is O(n).

Optimized Dynamic Programming: 
In this approach, apart from the dp table, we also maintain all the indexes which have matched earlier. Then we will check the substrings from those indexes to the current index. If anyone of that matches then we can divide the string up to that index.
In this program, we are using some extra space. However, its time complexity is O(n*n) if n>s or O(n*s) if s>n  where s is the length of the largest string in the dictionary and n is the length of the given string. 

C++

// A Dynamic Programming based program to test
// whether a given string can  be segmented into
// space separated words in dictionary
#include <bits/stdc++.h>
using namespace std;

/* A utility function to check whether a word
   is present in dictionary or not. An array of
   strings is used for dictionary.  Using array
   of strings for dictionary is definitely not
   a good idea. We have used for simplicity of
   the program*/
int dictionaryContains(string word)
{
    string dictionary[]
        = { "mobile", "samsung",  "sam",  "sung", "man",
            "mango",  "icecream", "and",  "go",   "i",
            "like",   "ice",      "cream" };
    int size = sizeof(dictionary) / sizeof(dictionary[0]);
    for (int i = 0; i < size; i++)
        if (dictionary[i].compare(word) == 0)
            return true;
    return false;
}

// Returns true if string can be segmented into space
// separated words, otherwise returns false
bool wordBreak(string s)
{
    int n = s.size();
    if (n == 0)
        return true;

    // Create the DP table to store results of subproblems.
    // The value dp[i] will be true if str[0..i] can be
    // segmented into dictionary words, otherwise false.
    vector<bool> dp(n + 1, 0); // Initialize all values
    // as false.

    // matched_index array represents the indexes for which
    // dp[i] is true. Initially only -1 element is present
    // in this array.
    vector<int> matched_index;
    matched_index.push_back(-1);

    for (int i = 0; i < n; i++) {
        int msize = matched_index.size();

        // Flag value which tells that a substring matches
        // with given words or not.
        int f = 0;

        // Check all the substring from the indexes matched
        // earlier. If any of that substring matches than
        // make flag value = 1;
        for (int j = msize - 1; j >= 0; j--) {

            // sb is substring starting from
            // matched_index[j]
            // + 1  and of length i - matched_index[j]
            string sb = s.substr(matched_index[j] + 1,
                                 i - matched_index[j]);

            if (dictionaryContains(sb)) {
                f = 1;
                break;
            }
        }

        // If substring matches than do dp[i] = 1 and
        // push that index in matched_index array.
        if (f == 1) {
            dp[i] = 1;
            matched_index.push_back(i);
        }
    }
    return dp[n - 1];
}

// Driver code
int main()
{
    wordBreak("ilikesamsung") ? cout << "Yes\n"
                              : cout << "No\n";
    wordBreak("iiiiiiii") ? cout << "Yes\n"
                          : cout << "No\n";
    wordBreak("") ? cout << "Yes\n" : cout << "No\n";
    wordBreak("ilikelikeimangoiii") ? cout << "Yes\n"
                                    : cout << "No\n";
    wordBreak("samsungandmango") ? cout << "Yes\n"
                                 : cout << "No\n";
    wordBreak("samsungandmangok") ? cout << "Yes\n"
                                  : cout << "No\n";
    return 0;
}

Java

import java.io.*;
import java.util.*;

class GFG {

  public static boolean wordBreak(String s, List<String> dictionary) {
        // create a dp table to store results of subproblems
        // value of dp[i] will be true if string s can be segmented
        // into dictionary words from 0 to i.
        boolean[] dp = new boolean[s.length() + 1];

        // dp[0] is true because an empty string can always be segmented.
        dp[0] = true;

        for(int i = 0; i <= s.length(); i++){
            for(int j = 0; j < i; j++){
                if(dp[j] && dictionary.contains(s.substring(j, i))){
                    dp[i] = true;
                    break;
                }
            }
        }
        return dp[s.length()];
    }

    public static void main (String[] args) {
      String[] dictionary = { "mobile", "samsung",  "sam",  "sung", "man",
                "mango",  "icecream", "and",  "go",   "i",
                "like",   "ice",      "cream" };

        List<String> dict = new ArrayList<>();
        for(String s : dictionary){
            dict.add(s);
        }

        if (wordBreak("ilikesamsung", dict)) {
            System.out.println("Yes");
        } else {
            System.out.println("No");
        }
        if (wordBreak("iiiiiiii", dict)) {
            System.out.println("Yes");
        } else {
            System.out.println("No");
        }
        if (wordBreak("", dict)) {
            System.out.println("Yes");
        } else {
            System.out.println("No");
        }
        if (wordBreak("samsungandmango", dict)) {
            System.out.println("Yes");
        } else {
            System.out.println("No");
        }
        if (wordBreak("ilikesamsung", dict)) {
            System.out.println("Yes");
        } else {
            System.out.println("No");
        }
        if (wordBreak("samsungandmangok", dict)) {
            System.out.println("Yes");
        } else {
            System.out.println("No");
        }

    }
}

Python3

def wordBreak(s, dictionary):

    # create a dp table to store results of subproblems
    # value of dp[i] will be true if string s can be segmented
    # into dictionary words from 0 to i.
    dp = [False for i in range(len(s) + 1)]

    # dp[0] is true because an empty string can always be segmented.
    dp[0] = True

    for i in range(len(s) + 1):
        for j in range(i):
            if dp[j] and s[j: i] in dictionary:
                dp[i] = True
                break

    return dp[len(s)]

# driver code
dictionary = [ "mobile", "samsung", "sam", "sung", "man", "mango", "icecream", "and", "go", "i", "like", "ice", "cream" ]

dict = set()
for s in dictionary:
    dict.add(s)

if (wordBreak("ilikesamsung", dict)):
    print("Yes")
else :
    print("No")

if (wordBreak("iiiiiiii", dict)):
    print("Yes")
else:
    print("No")

if (wordBreak("", dict)):
    print("Yes")
else:
    print("No")

if (wordBreak("samsungandmango", dict)):
    print("Yes")
else:
    print("No")

if (wordBreak("ilikesamsung", dict)):
    print("Yes")
else:
    print("No")

if (wordBreak("samsungandmangok", dict)):
    print("Yes")
else:
    print("No")

# This code is contributed by shinjanpatra

C#

using System;
using System.Collections.Generic;

public class WordBreakProgram {
    // A utility function to check whether a word
    // is present in dictionary or not. A HashSet of
    // strings is used for dictionary.
    static bool
    DictionaryContains(HashSet<string> dictionary,
                       string word)
    {
        return dictionary.Contains(word);
    }

    // Returns true if string can be segmented into space
    // separated words, otherwise returns false
    static bool WordBreak(string s,
                          HashSet<string> dictionary)
    {
        int n = s.Length;
        if (n == 0)
            return true;

        // Create the DP table to store results of
        // subproblems. The value dp[i] will be true if
        // str[0..i] can be segmented into dictionary words,
        // otherwise false.
        bool[] dp = new bool[n + 1];

        // matchedIndex array represents the indexes for
        // which dp[i] is true. Initially only -1 element is
        // present in this array.
        List<int> matchedIndex = new List<int>();
        matchedIndex.Add(-1);

        for (int i = 0; i < n; i++) {
            int msize = matchedIndex.Count;

            // Flag value which tells that a substring
            // matches with given words or not.
            int f = 0;

            // Check all the substring from the indexes
            // matched earlier. If any of that substring
            // matches than make flag value = 1;
            for (int j = msize - 1; j >= 0; j--) {
                // sb is substring starting from
                // matchedIndex[j]
                // + 1  and of length i - matchedIndex[j]
                string sb
                    = s.Substring(matchedIndex[j] + 1,
                                  i - matchedIndex[j]);

                if (DictionaryContains(dictionary, sb)) {
                    f = 1;
                    break;
                }
            }

            // If substring matches than do dp[i] = 1 and
            // push that index in matchedIndex array.
            if (f == 1) {
                dp[i] = true;
                matchedIndex.Add(i);
            }
        }
        return dp[n - 1];
    }

    // Driver code
    public static void Main()
    {
        HashSet<string> dictionary = new HashSet<string>{
            "mobile", "samsung",  "sam",  "sung", "man",
            "mango",  "icecream", "and",  "go",   "i",
            "like",   "ice",      "cream"
        };

        Console.WriteLine(
            WordBreak("ilikesamsung", dictionary) ? "Yes"
                                                  : "No");
        Console.WriteLine(WordBreak("iiiiiiii", dictionary)
                              ? "Yes"
                              : "No");
        Console.WriteLine(WordBreak("", dictionary) ? "Yes"
                                                    : "No");
        Console.WriteLine(
            WordBreak("ilikelikeimangoiii", dictionary)
                ? "Yes"
                : "No");
        Console.WriteLine(
            WordBreak("samsungandmango", dictionary)
                ? "Yes"
                : "No");
        Console.WriteLine(
            WordBreak("samsungandmangok", dictionary)
                ? "Yes"
                : "No");
    }
}
// This code is contributed by Rohit Yadav

Javascript

    <script>
    function wordBreak( s, dictionary)
    {

        // create a dp table to store results of subproblems
        // value of dp[i] will be true if string s can be segmented
        // into dictionary words from 0 to i.
        var dp = Array(s.length + 1).fill(false);

        // dp[0] is true because an empty string can always be segmented.
        dp[0] = true;

        for (var i = 0; i <= s.length; i++) {
            for (var j = 0; j < i; j++) {
                if (dp[j] && dictionary.has(s.substring(j, i))) {
                    dp[i] = true;
                    break;
                }
            }
        }
        return dp[s.length];
    }


        var dictionary = [ "mobile", "samsung", "sam", "sung", "man", "mango", "icecream", "and", "go", "i",
                "like", "ice", "cream" ];

        var dict = new Set();
        for (var s of dictionary) {
            dict.add(s);
        }

        if (wordBreak("ilikesamsung", dict)) {
            document.write("<br/>Yes");
        } else {
            document.write("<br/>No");
        }
        if (wordBreak("iiiiiiii", dict)) {
            document.write("<br/>Yes");
        } else {
            document.write("<br/>No");
        }
        if (wordBreak("", dict)) {
            document.write("<br/>Yes");
        } else {
            document.write("<br/>No");
        }
        if (wordBreak("samsungandmango", dict)) {
            document.write("<br/>Yes");
        } else {
            document.write("<br/>No");
        }
        if (wordBreak("ilikesamsung", dict)) {
            document.write("<br/>Yes");
        } else {
            document.write("<br/>No");
        }
        if (wordBreak("samsungandmangok", dict)) {
            document.write("<br/>Yes");
        } else {
            document.write("<br/>No");
        }

// This code is contributed by Rajput-Ji
</script>

Output

Yes
Yes
Yes
Yes
Yes
No

Word Break Problem | (Trie solution)
Exercise:
The above solutions only find out whether a given string can be segmented or not. Extend the above Dynamic Programming solution to print all possible partitions of input string.
Examples:

Input: ilikeicecreamandmango
Output: 
i like ice cream and man go
i like ice cream and mango
i like icecream and man go
i like icecream and mango
Input: ilikesamsungmobile
Output:
i like sam sung mobile
i like samsung mobile

Word Break Problem | (Hashmap solution):

In this approach first, we are storing all the words in a Hashmap. after that, we traverse the input string and check if there is a match or not. 

C++

#include<bits/stdc++.h>
using namespace std;
bool CanParseUtil(unordered_map<string, bool>mp, string word)
{
    // if the size id zero that means we completed the word. so we can return true
    int size = word.size();
    if(size == 0)
    {
        return true;
    }
    string temp = "";
    for(int i = 0; i < word.length(); i++)
    {
        temp += word[i];
        // if the temp exist in hashmap and the parsing operation of the remaining word is true, we can return true.
        if(mp.find(temp) != mp.end() && CanParseUtil(mp, word.substr(i+1)))
        {
            return true;
        }
    }
    // if there is a mismatch in the dictionary, we can return false.
    return false;
}
string CanParse(vector<string>words, string word)
{
    int start = 0;
    // store the words in the hashmap
    unordered_map<string, bool>mp;
    for(auto it : words)
    {
        mp[it] = true;
    }
    return CanParseUtil(mp,word ) == true ? "YES" : "NO";
}


int main() {
    vector<string>words{"mobile","samsung","sam","sung",
                            "man","mango","icecream","and",
                             "go","i","like","ice","cream"};
    string word = "samsungandmangok";
    cout << CanParse(words, word) << endl;
}

Java

import java.util.*;

class GFG {
  static boolean CanParseUtil(HashMap<String, Boolean> mp,
                              String word)
  {

    // if the size id zero that means we completed the
    // word. so we can return true
    int size = word.length();
    if (size == 0) {
      return true;
    }
    String temp = "";
    for (int i = 0; i < word.length(); i++) {
      temp += word.charAt(i);

      // if the temp exist in hashmap and the parsing
      // operation of the remaining word is true, we
      // can return true.
      if (mp.containsKey(temp)
          && CanParseUtil(mp,
                          word.substring(i + 1))) {
        return true;
      }
    }

    // if there is a mismatch in the dictionary, we can
    // return false.
    return false;
  }

  static String CanParse(String[] words, String word)
  {

    // store the words in the hashmap
    HashMap<String, Boolean> mp = new HashMap<>();
    for (String it : words) {
      mp.put(it, true);
    }
    return CanParseUtil(mp, word) == true ? "YES"
      : "NO";
  }

  public static void main(String[] args)
  {
    String[] words
      = { "mobile", "samsung",  "sam",  "sung", "man",
         "mango",  "icecream", "and",  "go",   "i",
         "like",   "ice",      "cream" };
    String word = "samsungandmangok";
    System.out.println(CanParse(words, word));
  }
}

// This code is contributed by karandeep1234.

Python3

def CanParseUtil(mp,word):

    # if the size id zero that means we completed the word. so we can return True
    size = len(word)
    if(size == 0):
        return True

    temp = ""
    for i in range(len(word)):

        temp += word[i]
        # if the temp exist in hashmap and the parsing operation of the remaining word is True, we can return True.
        if(temp in mp and CanParseUtil(mp, word[i+1:])):

            return True

    # if there is a mismatch in the dictionary, we can return false.
    return False

def CanParse(words,word):

    start = 0
    # store the words in the hashmap
    mp = {}
    for it in words:
        mp[it] = True

    return "YES" if CanParseUtil(mp,word ) == True else "NO"


# driver code

words = ["mobile","samsung","sam","sung",
         "man","mango","icecream","and",
         "go","i","like","ice","cream"]
word = "samsungandmangok"
print(CanParse(words, word))

# This code is contributed by shinjanpatra

C#

using System;
using System.Collections.Generic;

class Program {

    // Utility function to recursively check if a given word can be parsed from a dictionary of words
    static bool CanParseUtil(Dictionary<string, bool> mp, string word) {
        // If the size of the word is zero, that means we've completed the word, so we can return true
        int size = word.Length;
        if(size == 0) {
            return true;
        }
        string temp = "";
        // Iterate over each character in the word and check if we can form a valid word by adding the character to the prefix
        for(int i = 0; i < word.Length; i++) {
            temp += word[i];
            // If the prefix exists in the dictionary and the remaining portion of the word can also be parsed, return true
            if(mp.ContainsKey(temp) && CanParseUtil(mp, word.Substring(i+1))) {
                return true;
            }
        }
        // If there is a mismatch in the dictionary, we can return false
        return false;
    }

    // Main function to check if a given word can be parsed from a list of words
    static string CanParse(List<string> words, string word) {
        int start = 0;
        // Store the words in a dictionary for faster lookup
        Dictionary<string, bool> mp = new Dictionary<string, bool>();
        foreach(string it in words) {
            mp.Add(it, true);
        }
        // Call the utility function to check if the given word can be parsed from the dictionary
        return CanParseUtil(mp, word) == true ? "YES" : "NO";
    }

    static void Main(string[] args) {
        // Sample input words and word to be parsed
        List<string> words = new List<string> { "mobile", "samsung", "sam", "sung", "man", "mango", "icecream", "and", "go", "i", "like", "ice", "cream" };
        string word = "samsungandmangok";
        // Call the CanParse function to check if the given word can be parsed from the list of words
        Console.WriteLine(CanParse(words, word));
    }
}

Javascript

<script>

function CanParseUtil(mp,word)
{
    // if the size id zero that means we completed the word. so we can return true
    let size = word.length;
    if(size == 0)
    {
        return true;
    }
    let temp = "";
    for(let i = 0; i < word.length; i++)
    {
        temp += word[i];
        // if the temp exist in hashmap and the parsing operation of the remaining word is true, we can return true.
        if(mp.has(temp) === true && CanParseUtil(mp, word.substring(i+1)))
        {
            return true;
        }
    }
    // if there is a mismatch in the dictionary, we can return false.
    return false;
}
function CanParse(words,word)
{
    let start = 0;
    // store the words in the hashmap
    let mp = new Map();
    for(let it of words)
    {
        mp.set(it , true);
    }
    return CanParseUtil(mp,word ) == true ? "YES" : "NO";
}


// driver code

let words = ["mobile","samsung","sam","sung",
             "man","mango","icecream","and",
             "go","i","like","ice","cream"];
let word = "samsungandmangok";
document.write(CanParse(words, word),"</br>");

// code is contributed by shinjanpatra

</script>

Output

NO

Time Complexity: The time complexity of the above code will be O(2^n).
Auxiliary Space: The space complexity will be O(n) as we are using recursion and the recursive call stack will take O(n) space.

Refer below post for solution of exercise. 
Word Break Problem using Backtracking
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above