Why is a rhombus not a square?

You may have studied about squares and rhombuses in geometry class. These two forms share strange resemblance since they belong to the same family of parallelograms or quadrilaterals. The primary distinction between square and rhombus is that square has all of its angles equal to 90 degrees, but rhombus does not. However, all of the sides of both forms are equal. 

What is a Square?

A square is considered to be a regular quadrilateral, with all four sides having an equal length and all equal four angles. The angles subtended at the adjacent sides of a square are right angles. In addition to this, the diagonals of the square are equal and bisect each other at 90^o. A square is a special case of a parallelogram with two adjacent equal sides and one right vertex angle. Also, a square can be considered as a special case of a rectangle, with equal length and breadth. 

Properties of a Square

A square is a closed figure with the following properties: 

• A square is a closed quadrilateral with 4 sides and 4 vertices.
• All sides of a square are equal to each other.
• Lengths of both the diagonals is equal.
• The opposite sides are parallel to each other, therefore, it is called a parallelogram.
• The summation of interior angles of a rhombus is 360°.
• The diagonals of a square bisect each other at 90°.
• The diagonals divide the square into two congruent triangles.
• The opposite sides of a square are parallel to each other.
• The interior angle formed at each of the vertexes of a square is 90°.
• The length of the diagonal with sides s is √2 × s
• The length of the diagonals in a square is greater than its sides.

Area of the Square: The region enclosed within a two-dimensional plane is called the area of a figure. In the case of a square, the area is equivalent to the square of the sides. It is measured in a square units.

Area = (side)²

Let us assume ‘a’ to the length of the side of the square, then we have;

Area = a²

Perimeter of the Square: The sum of all four sides of a square is known as its perimeter. It is measure in the same unit as length. Thus, we know, 

Perimeter = 4 × Side of the Square 

Let us assume ‘a’ to the length of the side of the square, then we have;

Perimeter = 4 × a

Formula for Diagonal of the Square: Both the diagonals of a square are equal to each other. Let us assume ‘a’ to the length of the side of the square. By Pythagoras theorem, we have, 

Hypotenuse² = Base² + Perpendicular²

Hypotenuse² = a² + a²

Hypotenuse² = 2a² + Perpendicular²

Hypotenuse = a√2

The length of the diagonals of the square is equal to a√2. 

Diagonal is the hypotenuse and the two sides of the triangle are formed by diagonal of the square. 

Therefore, 

Diagonal² = Side² + Side²

Diagonal = √2(side)²

or

d = a√2

where d is the length of the diagonal of a square and a is the side.

What is a Rhombus?

A rhombus is also known as a four-sided quadrilateral. It is considered to be a special case of a parallelogram. A rhombus contains parallel opposite sides and equal opposite angles. A rhombus is also known by the name diamond or rhombus diamond. A rhombus contains all the sides of a rhombus is equal in length. Also, the diagonals of a rhombus bisect each other at right angles. 

Properties of a Rhombus

A rhombus contains the following properties: 

• A rhombus contains all equal sides.
• Diagonals of a rhombus bisect each other at right angles.
• The opposite sides of a rhombus are parallel in nature.
• The sum of two adjacent angles of a rhombus is equal to 180^o.
• There is no inscribing circle within a rhombus.
• There is no circumscribing circle around a rhombus.
• The diagonals of a rhombus lead to the formation of four right-angled triangles.
• These triangles are congruent to each other.
• The opposite angles of a rhombus are equal.
• When you connect the midpoint of the sides of a rhombus, a rectangle is formed.
• When the midpoints of half the diagonal are connected, another rhombus is formed.

Perimeter of Rhombus: The perimeter of a rhombus is defined as the total length of its boundaries forming the figure. It can also be denoted as the total summation of the length of four sides of a rhombus. The perimeter of a rhombus is defined by : 

Perimeter, P = 4a 

where the diagonals of the rhombus are denoted by d₁ & d₂ and ‘a’ is the side.

Area of Rhombus: The area of the rhombus is defined as the region enclosed within a two-dimensional plane. The area of a rhombus is equivalent to the product of diagonals of rhombus divided by 2. The area of the rhombus can be defined by the following formula: 

Area, A = (d₁ × d₂) / 2

Is Square a Rhombus? 

Squares and rhombuses hold some similarities and certain differences. Both the closed figures hold certain properties which differ in the number of their diagonals, length, shape and diagonals. Both the rhombus and square have similar properties since they both fall under the parallelogram category. 

However, rhombus and square have different properties: In a rhombus, one pair of opposite angles in a rhombus is acute, and another pair is obtuse. However, in case of a square, the four angles are each equal to 90o. Also, both the diagonals in a rhombus are of differing lengths. And, the diagonals in a square are identical in length.

Therefore, the square is always a rhombus but a rhombus may not necessarily be a square. 

A square is always a rhombus since all the sides of a square are equal in length. In addition to this, the diagonals of both the closed figures, square and rhombus are perpendicular to each other and bisect the opposite angles. Thus, a square is always a rhombus. 

Similar Questions

Question 1: Calculate the perimeter and area of the park with a side equal to 500 m?

Answer:

Here,

We have the length of one side of a square park = 500 m

So as the park is square all the sides of the parks are equal i.e 500 m.

Thus,

Perimeter of the Square park = 4 × side of the square park

= 4 × 500 = 2000 m

Hence, the perimeter of the park is 2000 m.

Now,

Area of the Square park = side² per square unit

side = 500 m

Area = 500² = 500 × 500 = 250000 sq. m

Question 2: We have a square park with a side equal to 12 cm. Calculate the area, perimeter and length of diagonal of the square.

Answer: 

Given, 

Side of the square, s = 12 cm

We know, 

Area of the square = Side²

Substituting the values, 

Area = 12 × 12 = 144 sq cm

The Area of the Square is 144 sq cm 

According to the formulae, we have, 

Perimeter of the square = 4 ×  side

Perimeter = 4 × 12 cm = 48 cm

Perimeter of the Square  = 48 cm

Length of the diagonal of square =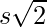 

Length of diagonal of the square = 12 × 1.414 = 16.9705 cm

Question 3: Find the length of the side of the square which has an area of 25 sq cm, Also find the perimeter of the Square?

Answer: 

We are given, 

Area of square = 25 sq.cm.

The area of square = side ² = s × s

Thus, 

On substituting the values, we get, 

We will get;

25 = side²

side = 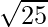 =  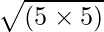= 5 cm

Therefore, 

The length of the side of the square is 5 cm.

Question 4: Differentiate between the closed figures, Rhombus and Square?

Answer:

Following are the difference between rhombus and Square as:

Square	Rhombus
A four-sided figure or parallelogram with 4 right angles meet at the vertex	A parallelogram whose opposite angles are equal in length.
The diagonals are equal in size	The diagonals are unequal in size
The sides are perpendicular to one another because all four angles of a square are equal to 90°	The sides are not perpendicular to one another because the opposite angles of a rhombus are equal in length.