Why diagonals of rhombus are not equal?
Last Updated :
12 Oct, 2021
Rhombus is a type of quadrilateral. Rhombus is the special case of a parallelogram, their diagonals intersect each other at 90°. It is also called a diamond because the shape of a rhombus is a diamond shape.
A quadrilateral is defined as a polygon having four sides and four vertices that enclose four angles. The Interior angle sum of any quadrilateral is 360°. They are of six types:
- Parallelogram
- Trapezium
- Square
- Rectangle
- Kite
- Rhombus
Rhombus
A rhombus can be defined as a special parallelogram or quadrilateral as it meets all the conditions of a parallelogram, a rhombus has all of its sides are equal and with two pairs of parallel sides, but it can be said that it is a type of parallelogram with four congruent sides. Therefore a rhombus fits all the properties of a parallelogram. We can notice in the figure below that all sides remain the same length and the opposite sides remain parallel.
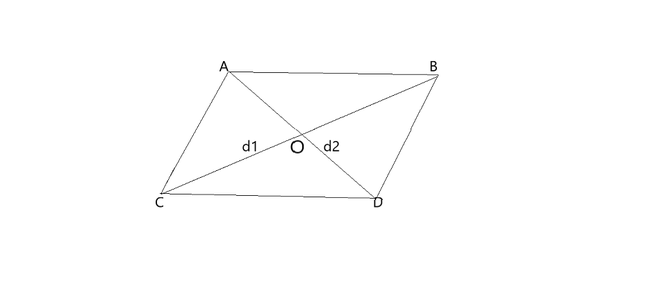
Rhombus
Is square a type of Rhombus?
- In Rhombus all of its sides are equal and Square also resemble this property.
- The diagonals of the square bisect the opposite angles and perpendicular to each other.
That’s why a square is a type of rhombus.
Formulae for Rhombus
Area of Rhombus
The area of the rhombus is the region covered inside the plane or inside the side. The area of a rhombus is given by:
Area of Rhombus = (d1 x d2)/2 square units
Show that the area of Rhombus is (d1 × d2)/2 square units
Proof:
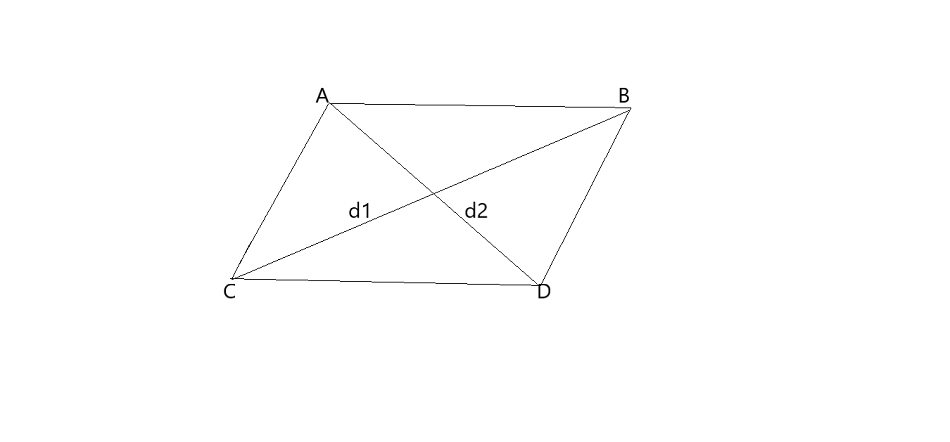
Consider a triangle ACD
Area of Triangle ACD = 1/2 × AD × d1/2 = 1/4 × CD × d1 — (Area of Triangle = 1/2 × base × height)
Area of Triangle ABD = 1/2 × AD × d2/2 = 1/4 × AB × d1
Area of Rhombus = Area of Triangle ACD + Area of Triangle ABD
= 1/4 × AD × d1 + 1/4 × AD × d1
= 1/4 × AD (d1 + d1)
= 1/4 × AD × 2d1
= 1/2(d1 × d2) (AD = d1)
Therefore, the area of Rhombus is (d1 × d2)/2 square units.
Perimeter of Rhombus
The perimeter of the Rhombus is the total length of boundaries covers in the length, or sum of all its four sides is called its perimeter.
Perimeter of Rhombus = 4a units
Properties of Rhombus
Following are the important properties of the rhombus as:

Properties of Rhombus based on this figure
- All four sides of the rhombus are equal (In the above fig. AB = BC = CD = DA).
- The opposite sides of a rhombus are parallel (In the above fig. AB //el CD and AC //el BD).
- Opposite angles of a rhombus are equal (∠C = ∠B and ∠A = ∠D).
- Diagonals bisect each other at right angles(∠COD = ∠DOB = ∠BOA = ∠AOC = 90°).
- Diagonals of Rhombus bisect the angles of a rhombus (all angles are equal during bisection).
- The sum of two adjacent angles is equal to 180 degrees (∠ACD + ∠CDB = 180°).
- Four right-angled triangles are formed through two diagonals of a rhombus which are congruent to each other
- If the midpoints of diagonals are joined together it will form another rhombus.
- There is not a possibility of circumscribing a circle around a rhombus.
- Also, there is no inscribing circle in the rhombus
- Where the midpoints of the all sides are joined together, there will be a rectangle, and the dimensions i.e. length and breadth of that rectangle of the main value of diagonal therefore the area of the rectangle is half of the rhombus.
Why diagonals of rhombus are not equal?
In rhombus, the diagonals are perpendicular bisectors to each other, but not equal in length. This means that diagonals cut each other in half.
In a special case of rhombus, if all 4 angles are equal to 90° each, then this is a case of square, where the diagonals are equal in measurement and perpendicular bisectors to each other.
Sample Question
Question 1: Find the area of Rhombus, given its diagonals are 9cm and 8cm.
Solution:
Area of Rhombus = (d1 × d2)/2
= (9 × 8)/2 = 72/2
= 36 cm2
Question 2: If the area of rhombus is 121 cm2 and the length measure of the longest diagonal is 22 cm, find the diagonal of a rhombus.
Solution:
Given,
Area of rhombus = 121 cm2
say d1 = 22 cm.
Area of the rhombus, A = (d1 × d2)/2
121 = (22 × d2)/2
121 = 11 × d2
or d2 = 11cm
Therefore, the Length of another diagonal is 11 cm.
Question 3: If perimeter of rhombus is 120 cm calculate its length.
Solution:
Perimeter of Rhombus = 4 × s
120 = 4 × s
or
s = 120/4 = 30
All sides of Rhombus are equal = 30 cm
Question 4: Find the perimeter of the rhombus if its diagonals are 20 and 48 cm.
Solution:
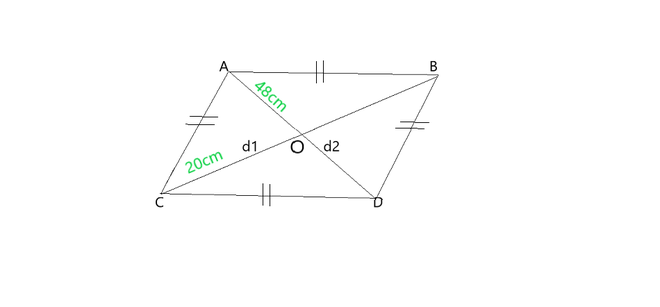
d1 = 20cm and d2 = 48cm
OA = AD/2 = 48/2 = 24cm
OC = BC/2 = 20/2 = 10cm
In triangle AOC
using pythagoras theorem
AC2 = OA2 + OC2
AC = √(24)2 + (10)2
AC = √576 + 100 = √676 = 26cm
Perimeter of rhombus = 4×side = 4×26 = 104cm
Question 5: Find the sides of Rhombus, whose area and altitude are 200cm2 and 40cm.
Solution:
Area of Rhombus = b × h
200 = b × 40
b = 200/40 = 5 cm
Question 6: Find the perimeter of rhombus, whose area is 315cm2 and altitude is 15cm.
Solution:
Area of rhombus = b × h
315 = b × 15
b = 315/15 = 21 cm
Perimeter of rhombus = 4×side = 4×21 = 84cm
Question 7: Find the altitude of a rhombus whose area and perimeter are 315cm2 and 180cm2 respectively.
Solution:
Perimeter of rhombus = 180cm
4×s = 180
s = 45cm
Area of rhombus = b × h
315 = 45 × h
h = 315/45
h = 7cm
Share your thoughts in the comments
Please Login to comment...