Wheel Graph using Networkx Python

A wheel graph is a type of graph in which if we connect each node in an n-1 node cycle graph to nth node kept at the centre we get a wheel graph. The definition would be more clear after seeing the example below.

Wheel Graph with n nodes is represented by W_n .

Example:

W₅:

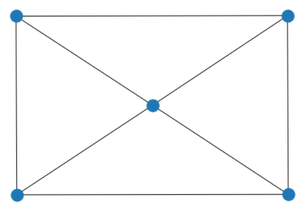
W₅

 W₆:

W₆

Properties of Wheel Graph:

• Total number of edges are 2(N-1)
• It is a planar graph.
• The diameter of the wheel graph is 2 if n>4 or 1 if n=4.
• It is a kind of Hamiltonian Graph.
• Wheel Graph with n nodes is represented by W_n .
• It is a cyclic graph.

We will use the networkx module for realizing a Wheel graph. It comes with an inbuilt function networkx.wheel_graph() and can be illustrated using the networkx.draw() method. This module in Python is used for visualizing and analyzing different kinds of graphs.

Syntax:

networkx.wheel_graph(n)

Parameters:

• N: Number of nodes in wheel graph.
• Returns a wheel graph object.

networkx.draw(G, node_size, node_color)

• Used to realize the graph by passing graph object.
• G: It refers to the Wheel graph object
• node_size: It refers to the size of nodes.
• node_color: It refers to color of the nodes.

Approach:

• We will import the required module network
• We will set the number of nodes or n=5.
• Then we will create a graph object using networkx.wheel_graph(n).
• For realizing the graph, we will use networkx.draw(G).
• This will print the required wheel graph.

Implementation:

Python3

# import required module
import networkx

# number of nodes
n = 5

# create object
G = networkx.wheel_graph(n)

# illustrate graph
networkx.draw(G)

Output:

Explanation:

As we initialized n=5 the wheel graph with 5 nodes with a cycle graph having 4 nodes and a central node connected to all other nodes is printed using networkx inbuilt draw function.