What will happen to the volume of a cuboid if its length is doubled, height is same, and breadth is halved?
Last Updated :
29 Feb, 2024
Cuboid is a three-dimensional solid object. It is also referred to as a regular hexahedron and is one of the five platonic solids. All the edges share at least a common edge with each other. The structure of a cuboid can be defined in terms of the fact that each of the faces is being connected to four vertices and four edges, vertex connected with three edges and three faces, and edges are in touch with two faces and two vertices. The length, breadth, or height may or may not be equal in the case of a cuboid.
Properties of Cuboid
- All the faces are rectangular in nature.
- All the angles are at right angles
- The opposite faces of a cuboid are equal.
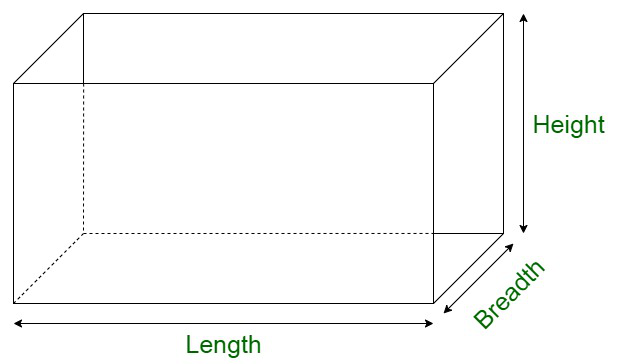
Volume of Cuboid
The volume of a cuboid is equivalent to the amount of space occupied within the figure. The volume of any three-dimensional figure is dependent on the three edges’ length, that is, its length, breadth, and height. It can be considered to be a solid rectangle. Let us assume the height of the cuboid to be h, l its length and breadth to be denoted by b units respectively.
In addition to this, let us assume V to be the volume of the cuboid. Deriving its formula,
The volume of cuboid = Base area × Height
The base area for cuboid = l × b
Volume of a cuboid, V = l × b × h = lbh
Also,
Volume of the cuboid = Area of cuboid × Height
What will happen to the volume of a cuboid if its length is doubled, height is the same, and breadth is halved?
Solution:
Let us assume l to be the length of cuboid and b to be its breadth. Also, let us assume h to be the height of the cuboid.
So,
Volume of a cuboid = l × b × h
Now,
Length of a cuboid becomes = 2l
Breadth = b/2
Height = h
Volume of cuboid , on simplifying becomes,
2l × b/2 × h
= l × b × h
Therefore, the final volume of the cuboid remains same.
Sample Questions
Question 1. If volume of a cuboid is 24000 cm3. Then find the change in the volume if its length is doubled, height is the same and breadth is halved?
Solution:
Here we have to find the volume change in the cuboid if the dimensions are changed
Volume of cuboid = l × b × h = 24000 cm3
Changed dimensions
l = 2l
b = 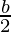
h = h
Therefore,
Changed dimensions volume = 2l ×  × h
× h
Further simplifying
Changed dimensions volume = l × b × h
Thus, we can clearly see that there is no change in the dimensions
As the dimensions are same
Therefore,
Volume of cuboid is also same that is 24000 cm3.
Question 2. If the volume of the cuboid is 3000 m3 and its length is 20 m breadth is 15 m, then find the height of the cuboid?
Solution:
Here we have to find the height of the cuboid using its volume and 2 dimensions
As we know that,
Volume of cuboid = l × b × h
According to the question
Volume of cuboid = 3000 m3
Substituting value of volume of cuboid
3000 = l × b × h
3000 = 20 × 15 × h
h = 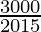
h = 10 m
Therefore,
Height of the cuboid is 10 m.
Question 3. Consider the length of a cuboid is double its breadth, breadth of cuboid is double of its height, and volume of the cuboid is 8000 m3. Find all the dimensions of the cuboid?
Solution:
Here we have to find the dimensions of the cuboid by using the given volume 8000 m3.
Assume that the height of the cuboid is ‘x’.
According to the question,
Breadth of cuboid is double its height,
So, Breadth = 2 × height = 2 × x = 2x
And, Length of cuboid is double its breadth,
So, Length = 2 × breadth = 2 × 2x = 4x
Therefore,
Length = 4x,
Breadth = 2x
Height = x
As we know that,
Volume of cuboid = l × b × h
Volume of cuboid = 4x × 2x × x
8000 = 8x3
x3 = 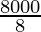
x3 = 1000
x = ![Rendered by QuickLaTeX.com \sqrt[3]{1000}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d06b07db634bc3a0e52908d4af7f93fd_l3.png)
x = 10 m
Hence,
Height of the cuboid = x = 10 m
Breadth of the cuboid = 2x = 2 × 10 = 20 m
Length of the cuboid = 4x = 4 × 10 = 40 m
Question 4. Assume that the breadth of the cuboid is halved, then find how much the volume of cuboid changes?
Solution:
Here we have to find the change in volume of the cuboid if its breadth is halved
As we know that
Volume of cuboid = length × breadth × height
According to the question
The breadth is halved
So, b = 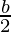
Therefore,
Volume of cuboid = l ×  × h
× h
Volume of cuboid = 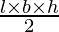
Volume of cuboid =  .
.
Hence,
We can see that the volume of the cuboid gets halved if its breadth gets halved.
Question 5. Calculate the amount of water in m3 that can be filled in a water tank of length 50 m breadth 40 m and height 10 m?
Solution:
Here we have to find the amount of water that can be filled in a water tank of dimensions,
Length = 50 m
Breadth = 40 m
Height = 10 m
As we know that
Volume of cuboid = length × breadth × height
Volume of cuboid = 50 × 40 × 10
Volume of cuboid = 20000 m3
Therefore,
20000 m3 water can be filled in the water tank.
Share your thoughts in the comments
Please Login to comment...