What is the probability that the sum of outcome is prime when two dice are rolled simultaneously?
Last Updated :
18 Nov, 2021
In mathematics, permutation refers to the act of organizing a set in which all the members of a set are arranged into some sequence or order. In other words, if the set is already arranged, then the rearranging of its component is called the process of permuting. Permutations take place, in more or less important ways, in almost every area of mathematics. They frequently appear when different commands on certain finite sets are considered.
What is a Combination?
A combination is an act of choosing items from a group, such that (unlike permutations) the order of choice does not matter. In smaller cases, it is possible to count the number of amalgamations. Combination refers to the amalgamation of n things taken k at a time without repetition. To refer to combinations in which reoccurrence is permitted, the terms k-selection or k-combination with repetition are frequently used.
Permutation Formula
A permutation is the choice of r things from a set of n things without replacement and where the sequence matters.
nPr = (n!)/(n-r)!
Combination Formula
A combination is the choice of r things from a set of n things without replacement and where order does not matter.
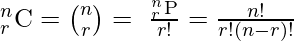
What is the probability that the sum of outcome is prime when two dice are rolled simultaneously?
Solution:
The total number of possible outcomes in this case is 36-
{(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),(3,1),(3,2),
(3,3),(3,4),(3,5),(3,6),(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),(5,1),(5,2),(5,3),(5,4),
(5,5),(5,6),(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)}
Out of the listed possibilities, the favorable outcomes are-
{(1,1),(1,2),(1,4),(1,6),(2,1),(2,3),(2,5),(3,2),(3,4),(4,1),(4,3),(5,2),(5,6),(6,1),
(6,5)}
Hence, the number of favorable outcomes is 15.
Therefore, the required probability is 15/36 = 5/12
Similar Questions
Question 1: How many outcomes are possible when three dice are rolled, if no two of them may be the same?
Solution:
The first two dice together have 6×5=30 possible outcomes, from above.
For each of these 30 outcomes, the third die has four possible outcomes,
So the total number of outcomes is 30×4=6×5×4=120. (Note that we consider the dice to be detectable,
that is, a roll of 6, 4, 1 is unlike than 4, 6, 1, because according to the question the first and second dice are different in the two rolls, even though the numbers as a place are similar.)
Question 2: Suppose blocks numbered 1 through n are in a barrel; we pull out k of them, placing them in a line as we do. How many outcomes are possible? That is, how many different arrangements of k blocks might we see?
Solution:
This is essentially the same as the previous question: there are k “spots” to be filled by blocks. Any of the n blocks might seem first in the line; then any of the remaining n−1 might seem next, and so on. The number of outcomes is thus
n(n−1)(n−2)⋯(n−k+1), by the multiplication principle. In the previous question, the first “spot” was die number one, the second spot was die number two, the third spot die number three, and 6⋅5⋅4=6(6−1)(6−2); notice that 6−2=6−3+1
Share your thoughts in the comments
Please Login to comment...