What is the probability of rolling a 1 on a dice three times in a row?

Last Updated : 20 Oct, 2021

Probability is a branch of mathematics that deals with the happening of a random event. Probability is used in Maths to predict how likely events are to happen. The probability of an event is between 0 and 1 only and can also be written in percentage.

The probability of event B is often written as P(B). Here P represents the possibility and B represents the event.

Whenever we are not sure about the outcome of an event, we take help of the probabilities of certain outcomes—how likely they occur. To understanding probability we take an example as tossing a coin:

There are two possible outcomes—heads or tails.

The probability of getting heads is half. You might already know that the likelihood is half/half or 50% as the event is an equally likely event and is complementary so the possibility of getting heads or tails is the same in this case which is 50%.

Formula of Probability

$Probability \space of\space an\space event = \frac{Number\space of\space ways\space it\space can\space occur}{Total\space number\space of\space outcomes}$

$P(A) = \frac{Number\space of\space ways\space A\space occurs}{Total\space number\space of\space outcomes}$

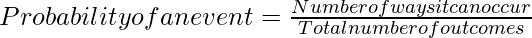
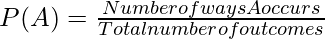
Equally Likely Events

Rolling a dice the probability of getting any of the numbers is 1/6. As the event is an equally likely event so the possibility of getting any number is the same in this case it is 1/6 in fair dice rolling.

Complementary Events

Possibility of only two outcomes which is an event will occur or not. Like a person will run or not run the race, buying a car or not buying a car, etc. are examples of complementary events.

What is the chance of rolling a 1 on a dice three times in a row?

Solution:

Probability of an event = (number of favorable event) / (total number of event).

P(B) = (Event B) / (total number of event).

Probability of getting 1 = 1/6.

Rolling dice is an independent event, it is not dependent on how many times it’s been rolled.

Probability of getting 1 three times in a row = probability of getting 1 first time × probability of getting 1 second time × probability of getting 1 third time.

Probability of getting 1 three times in a row = (1/6) × (1/6) × (1/6) = 1/216.

Hence, the probability of getting 1 three times in a row is 0.463%.

Similar Question

Question 1. What is the chance of rolling a 2 three times in a row?

Solution:

Probability of an event = (number of favorable event) / (total number of event).

P(B) = (Event B) / (total number of event).

Probability of getting 2 = 1/6.

Rolling dice is an independent event, it is not dependent on how many times it’s been rolled.

Probability of getting 2 three times in a row = probability of getting 2 first time×probability of getting 2 second time×probability of getting 2 third time.

Probability of getting 2 three times in a row = (1/6) × (1/6) × (1/6) = 1/216.

Hence, the probability of getting 2 three times in a row is 0.463%.

Question 2. What is the chance of rolling a 1 two times in a row?

Solution:

Probability of an event = (number of favorable event) / (total number of event).

P(B) = (Event B) / (total number of event).

Probability of getting 1 = 1/6.

Rolling dice is an independent event, it is not dependent on how many times it’s been rolled.

Probability of getting 1 two times in a row = probability of getting 1 first time×probability of getting 1 second time.

Probability of getting 1 two times in a row = (1/6) × (1/6) = 1/36.

Hence, the probability of getting 1 two times in a row 2.77 %.