A probability is a number that expresses the chance or likelihood of an event occurring. Probabilities can be stated as proportions ranging from 0 to 1, as well as percentages ranging from 0% to 100%, where 0 indicates an impossible event and 1 indicates a certain event. The sum of the probabilities of all the events in a sample space adds up to 1.
There are numerous applications of probability in real life. It is widely used in weather forecasting, typing on smart devices, flipping a coin or dice, sports, traffic signals, video games, and board games in taking medical decisions.
Formula for computing probability
P(E)=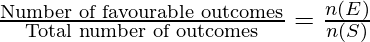
where,
P(E) is the Probability of an event E,
n(E) is the number of favorable outcomes
n(S) is the total number of outcomes in the sample space
Terms related to probability
Random Experiment: The action of achieving a set of possible outcomes without any prior conscious decision is called as a Random experiment. The prediction of a certain outcome of a random event is known as probability. Random trials include, for example, tossing a coin, drawing a card from a deck, and rolling a dice.
Outcome: An outcome is the result of any random experiment. Suppose if we roll a dice and we get a five. So, rolling a die is a random experiment that yielded the result “five”.
Sample space: It’s a collection of all plausible outcomes from a random experiment. For example, we can get one of the following numbers while rolling a die: 1, 2, 3, 4, 5, 6. As a result, the sample space consists of 1, 2, 3, 4, 5, and 6. This means that if a die is tossed, there are six sample spaces or probable outcomes.
Event: It is the result of a single experiment. Getting a Heads when tossing a coin is an example of an event.
Types of events:
- Complementary events: The likelihood that there will only be two outcomes, one of which states whether or not an event will take place. Complementary occurrences include things like today will either rain or not rain, the student will either pass or fail the exam, getting a job or not getting a job, and so on. In other words, the probability of an event occurring in the exact opposite direction of the probability of it not occurring.
- Mutually exclusive events: Mutually exclusive events are those in which the occurrence of one event precludes the occurrence of another, i.e. two events have no common point. For example, if S = 1, 2, 3, 4, 5, 6, and E1, E2 are two events, E1 consists of numbers less than 3 and E2 consists of numbers higher than 4, then E1 consists of numbers less than 3 and E2 consists of numbers greater than 4. As a result, E1 = 1,2 and E2 = 5,6. E1 and E2 are hence mutually exclusive events.
- Independent events: Independent events are ones whose occurrence is not contingent on the occurrence of another event. For instance, suppose we flip a coin in the air and obtain the result head, then flip the coin again and get the result Tail. The occurrence of these occurrences is independent of one another in both circumstances.
- Impossible and Sure Events: An event is called an impossible event if the probability of occurrence is zero, and a sure event if the probability of occurrence is one. To put it another way, the empty set is an impossible event, whereas the sample space S is a sure event.
- Exhaustive Events: When all of the events in a set use the whole sample space, it is said to as exhaustive.
- Simple Events: In probability, a simple event is an event that consists of a single point in the sample space. For instance, if S = 20, 98, 67, 14, 37 and E = 67, E is a simple event.
- Compound Events: A compound event is defined as an event that comprises of more than one single point in the sample space. In the same example, if S = 20, 98, 67, 14, 37, E1 = 20, 67, E2 = 98, 14, 37, E1 and E2 indicate two compound events.
- Event E1 but not E2: It symbolizes the distinction between the two occurrences. All the outcomes that are present in E1 but not in E2 are represented by the event E1 but not E2. As a result, the event E1 but not E2 is represented as E1 – E2.
- Events Associated with “AND”: If AND is associated with two events E1 and E2, it signifies that the intersection of elements common to both events has occurred. In probability, AND is represented by the intersection symbol (∩). E1 and E2 are thus represented by the event E1∩ E2.
- Events Associated with “OR”: If OR is related to two events E1 and E2, it signifies that either E1 or E2 or both are true. In probability, the union symbol (U) is used to indicate OR. As a result, the event E1 U E2 stands for E1 OR E2.
Equally likely events
Equally likely events occur when two or more events have the same theoretical likelihood of occurring. If all of the outcomes of a sample space have the same probability of occurring, they are said to be equally likely. If we throw a dice, for example, the probability of obtaining 1 is 1/6. Similarly, receiving all of the numbers from 2,3,4,5, and 6 one by one has a probability of 1/6. Some other instances of equally likely outcomes when rolling a die are as follows:
- Obtaining 2 and 4 on a die toss
- Using a die to obtain an even and an odd number
What is the probability of getting either a red card or King card?
We know that a well-shuffled deck has 52 cards
Total number of suits = 4
Total number of red suits = 2
Since each suite has 13 cards, therefore, the total number of red cards = 2 × 13 = 26
Therefore probability of getting a red card= 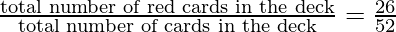
Total number of kings in a deck = 4
If we pick one card at random from the 52 cards, the probability of getting a king= 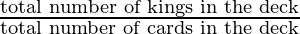
i.e. Probability of getting a king = 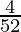
Therefore, probability of getting a red card or a king, P(E) = probability of getting a red card+ probability of getting a king
But out of these four kings, two kings are of the red suite and two are of the black suite. This means the probability of getting a red king has been included twice, and hence it should be subtracted.
Hence, probability of getting a red card or a king, P(E) = probability of getting a red card+ probability of getting a king-probability of getting a red king card=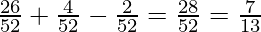
Similar Questions
Question 1. Find the probability of getting a black queen or a diamond
Answer:
Total number of cards=52
No. of favorable cards that are black queen = 2
Therefore probability of getting a black queen= 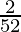
Total number of cards that are diamond=13
Therefore probability of getting a diamond= 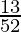
Therefore, probability of getting a red ace or a spade, P(E) = probability of getting a black queen+ probability of getting a diamond =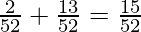
Question 2. Find the probability of getting either a black or a jack or an ace card
Answer:
Total number of cards=52
Total number of black cards = 26
Total number of jack cards = 4
Total number of ace cards = 4
probability of getting either a black or a jack or an ace card, P(E) = probability of getting a black card + probability of getting a jack + probability of getting an ace card-probability of getting a black jack card-probability of getting a black ace card = 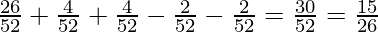
Question 3. Find the probability of getting an ace or a king
Answer:
Total number of cards in a deck=52
Total number of aces = 4
Total number of kings = 4
Therefore, probability of getting a king or a queen, P(E) = probability of getting an ace + probability of getting a king = 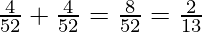
Question 4. Find the probability of getting red face cards
Answer:
Face cards are cards that are either, king, queen or jack
Total number of red king cards=Total number of red queen cards=Total number of red jack cards=2
Therefore, total number of red face cards=2+2+2=6
Therefore, probability of getting a red face card=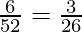
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...