What is the perimeter of an equilateral triangle whose height is 30cm?

In mathematics, the proportions, measurements, dimensions, forms, shapes, and angles of different objects around us are studied under the branch called geometry. Geometry is one of the oldest branches of mathematics and has a very significant application and impact on our daily lives. We are surrounded by innumerable objects in our lives. All these objects possess a certain shape, take up significant space, can be used to store a particular amount of things in them, and can be placed in different positions. All these factors fall under the scope of geometry. Shapes can be categorized a two- dimensional and three-dimensional. 

Equilateral Triangle

An equilateral triangle has all three sides of equal lengths and all three angles of equal measure, i.e., 60°. The figure below depicts an equilateral triangle ABC with ∠A = ∠B = ∠C = 60°.

Perimeter

The perimeter of a triangle is the sum of the lengths of all three sides. Since the lengths of sides of an equilateral triangle are equal, 

Perimeter of an equilateral side = 3 × Side.

Altitude of an Equilateral Triangle

The altitude or height of an equilateral triangle is the line segment that joins its upper vertex with its base. In the figure below, AD is the altitude of the triangle ABC because it joins the vertex A with the base BC.

The altitude of an equilateral triangle divides the given triangle into two congruent right triangles. It also bisects the base. This implies that if the length of the altitude or the side is given, the other length can be calculated using the Pythagoras Theorem.

Let the side of the triangle be a units. Then in right triangle ABD, 

AB² = AD² + BD²

⇒ 

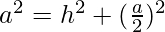
Thus, the height h of an equilateral triangle of side a is given by:

h =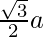 

What is the perimeter of an equilateral triangle whose height is 30 cm?

Solution:

In an equilateral triangle, h = .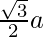

Here, h = 30 units.

⇒ a = 

= 34.64 cm.

Perimeter of the triangle = 3 × Side 

= 3 × 34.64 

= 103.92 cm

Similar Questions

Question 1: What is the perimeter of an equilateral triangle with a height of 15 cm?

Solution:

In an equilateral triangle,  h = .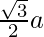

Here, h = 15 units.

⇒ a =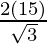 

= 17.320 cm.

Perimeter of the triangle = 3 × Side 

= 3 × 17.320 cm

= 51.96 cm.

Question 2: What is the perimeter of an equilateral triangle with a height of 9 cm?

Solution:

In an equilateral triangle,  h =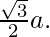 

Here, h = 9 units.

⇒ a =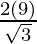 

= 10.39 cm.

Perimeter of the triangle = 3 × Side 

= 3 × 10.39

= 31.17 cm.

Question 3: What is the perimeter of an equilateral triangle with a height of 6 cm?

Solution:

In an equilateral triangle,  h =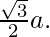 

Here, h = 6 units.

⇒ a =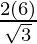 

= 6.92 cm.

Perimeter of the triangle = 3 × Side 

= 3 × 6.92

= 20.76 cm.

Question 4: What is the perimeter of an equilateral triangle with a height of 90?

Solution:

In an equilateral triangle,  h =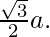 

Here, h = 90 units.

⇒ a =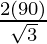 

= 103.92 cm.

Perimeter of the triangle = 3 × Side 

= 3 × 103.92

= 311.76 cm.

Question 5: What is the perimeter of an equilateral triangle with a height of 120?

Solution:

In an equilateral triangle,  h =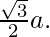 

Here, h = 120 units.

⇒ a =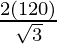 

= 138.56 cm.

Perimeter of the triangle = 3 × Side 

= 3 × 138.56

= 415.68 cm.

Question 6: What is the perimeter of an equilateral triangle with a height of 3?

Solution:

In an equilateral triangle,  h = \frac{\sqrt{3}}{2}a.

Here, h = 3 units.

⇒ a = 

= 3.46 cm.

Perimeter of the triangle = 3 × Side

= 3 × 3.46

= 10.38 cm.

Question 7: What is the perimeter of an equilateral triangle with a height of 18?

Solution:

In an equilateral triangle,  h = .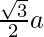

Here, h = 18 units.

⇒ a = \frac{2(18)}{\sqrt{3}}

= 20.78 cm.

Perimeter of the triangle = 3 × Side

= 3 × 20.78

= 62.34 cm.