What is the distance of the point (4, 3) from the origin?
Last Updated :
28 Feb, 2024
Geometry is undeniably one of the most important branches in the field of mathematics. Its significance is as profound as that of arithmetic and algebra, as much in our daily lives, as much as in the technicalities and intricacies of mathematics. Geometry, in daily lives, is basically prevalent everywhere. It is applied in designing a simple tiffin box to a mobile phone or a laptop to a water tank or even a bus, truck, and even dams. Hence anything which occupies space and has a definite shape has to be covered under the scope of geometry. In mathematical theory and problems too, the concept of geometry is employed to find the distance between two shapes, the space they take up, their sizes, and positions.
Coordinate Plane
Such a plane which is formed by the intersection of two lines, one of them being vertical and the other one horizontal, is called a co-ordinate plane in mathematics. It is a two- dimensional plane, with the vertical line being regarded as its y-axis and the horizontal one as the x-axis. The point of intersection of the two lines in the plane is called origin and is denoted by O. The figures on a match grid are used to detect points. A coordinate plane can be used to graph points, lines, and much further. It acts as a chart and yields precise directions from one point to another.
Coordinates
Coordinates are a group of two values that locate a selected point on a coordinate plane grid, better referred to as a coordinate plane. A point inside a coordinate plane is known by its ordered pair (x, y), written in parentheses, like the X-coordinate and therefore the Y-coordinate. These coordinates are often positive, zero, or negative, depending on their position within the respective quadrants.
Signs of Coordinates in Different Quadrants
The coordinate plane gets divided into 4 quadrants with the x-axis and y-axis. The first quadrant is the uppermost right one where both the x and y coordinates are positive numbers; the second quadrant lies to the left of the first where the x coordinate is positive and the y coordinate is negative; the third quadrant lies directly below the second quadrant where the x coordinate is negative and the y coordinate is positive; the fourth quadrant lies directly below the first quadrant and to the right of the third quadrant where both the x and y coordinates are negative.

Distance Formula
Distance in simple words is the quantification of how far apart two things/ objects/ points are. So clearly distance formula would be a mathematical equation for finding out the distance between two objects/ points, given their coordinates. It is to be noted that the points in question need not belong to the same quadrant. In mathematics, the distance formula is exclusively used in the coordinate system to find out how far apart two points are from each other in a coordinate plane with the help of their coordinates, thus having great importance in the field of geometry.

Suppose there are two points, A and B in a coordinate plane, first quadrant for the sake of simplicity. The coordinates of point A are (a,b) and B are (p,q). The distance between points A and B, denoted AB shall be given by:
AB = 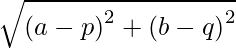
Derivation of Distance Formula

The formula is a direct application of the Pythagorean Theorem. The right triangle ASJ, with its hypotenuse AB would represent the required distance between the two points.
By Pythagoras Theorem,
AB2 = AJ2 + BJ2
= (a-p)2+(b-q)2
AB = 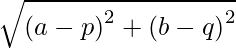
Distance of a Point From The Origin
Let the coordinates of the point be (x,y). The coordinates of origin are (0,0).
Using distance formula, we have:
d = 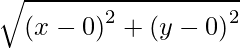
Distance of a point from the origin = 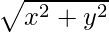
What is the distance of the point (4, 3) from the origin?
Solution:
We know, distance of a point from the origin = 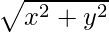
Hence, required distance = 
= 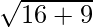
= 5
Thus, the distance of the point (4, 3) from the origin is 5 units.
Similar Problems
Question 1. Calculate the distance of the point (-100,0) from the origin.
Solution:
We know, distance of a point from the origin = 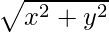
Hence, required distance = 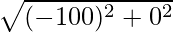
= 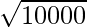
= 100
Thus, the distance of the point (-100,0) from the origin is 100 units.
Question 2. Calculate the distance of the point (9,5) from (4,5).
Solution:
Using distance formula, the distance between A(a,b) and B(p,q) is
AB = 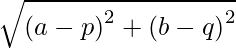
Hence required distance = 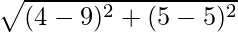
= 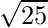
= 5
Thus, the distance of the point (9,5) from (4,5) from the origin is 5 units.
Question 3. Calculate the distance of the point (8,6) from the origin.
Solution:
We know, distance of a point from the origin = 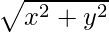
Hence, required distance = 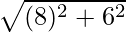
= 
= 10
Thus, the distance of the point (8,6) from the origin is 10 units.
Question 4. Calculate the distance of the point of (5,12) from the origin.
Solution:
We know, distance of a point from the origin = 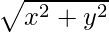
Hence, required distance = 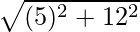
= 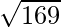
= 13
Thus, the distance of the point (5,12) from the origin is 13 units.
Question 5. Calculate the distance of the point (3,5) from (1,2).
Solution:
Using distance formula, the distance between A(a,b) and B(p,q) is
AB = 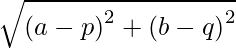
Hence required distance = 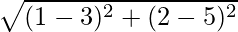
= 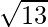
Thus, the distance of the point (3,5) from (1,2) from the origin is 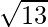 units.
units.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...