What is Rhombus?
Last Updated :
15 Nov, 2022
A Rhombus is a Parallelogram whose four sides all have the same length. Also called an equilateral quadrilateral. The figure represents a Rhombus.
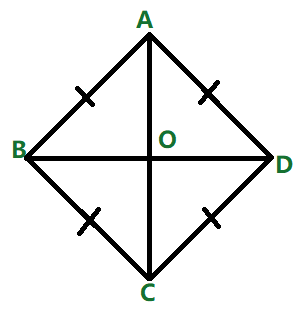
Properties
- All sides of the rhombus are equal.
- The opposite sides of a rhombus are parallel.
- The opposite angles of a rhombus are equal.
Properties of Diagonals of Rhombus
- In a rhombus, diagonals bisect each other at right angles.
- Diagonals bisect the angles of a rhombus.
To Prove
1. If a quadrilateral is a rhombus, then the diagonals are perpendicular bisectors of each other.
First, we will prove that the diagonals bisect each other then we will prove that the diagonals are perpendicular to each other.
(a) Diagonals bisect each other

Proof:
Since the rhombus is a parallelogram so the opposite sides are parallel and equal to each other.
So in the triangle AOD and COB we have
AD = CB ( opposite sides)
∠ADO = ∠CBO (opposite angles)
∠DAO = ∠BCO (opposite angles)
Hence both the triangles are congruent.
Hence AO = CO and DO = BO.
Hence the diagonals bisect each other.
(b) Diagonals are perpendicular to each other
Proof:
Given that ABCD is a rhombus
AB = AD (definition of rhombus)
AO = AO (Common side)
BO = OD (diagonals bisect each other as proved above)
△AOD ≅ △AOB (Side-Side-Side postulate)
∠AOD ≅ ∠AOB (Corresponding angles in congruent triangles )
Also ∠AOD + ∠AOB = 180
Hence AC ⊥ DB.
Hence the diagonals are the perpendicular bisector of each other.
2. The area of the rhombus is equal to half of the product of the diagonals.
Proof:
Given that ABCD is a rhombus the diagonal AC and BD cut at point O.

Now we know that ∠AOD = ∠AOB = ∠COD = ∠BOC = 90 degree.
Hence we can see that the rhombus ABCD is equally into four parts.
So the area of rhombus ABCD = area of triangle AOD + area of triangle AOB + area of triangle BOC + area of triangle COD.
1/2 × AO × OD + 1/2 × AO × OB + 1/2 × BO × OC + 1/2 × OD × OC
= 1/2 × AO (OD + OB) + 1/2 × OC (BO + OD)
= 1/2 × (OD + OB) × (AO + OC)
Hence the area of the rhombus is equal to half of the product of diagonals.
Examples
Example 1: Calculate the area of a rhombus whose diagonals are of the length 20 cm and 10 cm?
Solution:
We are Provided that
d1 = 20 cm
d2 = 10 cm
Area of a rhombus, A = (d1 × d2) / 2
= (20 × 10) / 2
= 100 cm2
Hence, the area of a rhombus is 100 cm2.
Example 2: Find the area of the rhombus having each side equal to 25 cm and the length of one of its diagonals is equal to 14 cm?
Solution:
ABCD is a rhombus in which AB = BC = CD = DA = 25 cm
AC = 14 cm
Area of rhombus = 1/2 * d1 * d2

Therefore, BO = 7 cm
In ∆ AOB,
AB² = AO² + OB²
⇒ 25² = 7² + OB²
⇒ 625 = 49 + OB²
⇒ 576 = OB²
⇒ OB = 24
Therefore, BD = 2 x OB = 2 × 24 = 48 cm
Now, area of rhombus = 1/2 × d₁ × d₂ = 1/2 × 14 × 48 = 336 cm²
Hence the area of the rhombus is 336 cm2.
Example 3: Find the height of the rhombus whose area is 400 m² and the perimeter is 160 m?
Solution:
Given, the perimeter of the rhombus = 160 m
So, side of rhombus = 160/4 = 40 m
We know that the area of any parallelogram = b × h
Therefore the height is:
⇒ 400 = 40 × h
⇒ h = 10 m
Therefore, the height of the rhombus is 10 m.
Share your thoughts in the comments
Please Login to comment...