What is Padding in Neural Network?

As we know while building a neural network we are doing convolution to extract features with the help of kernels with respect to the current datasets which is the important part to make your network learn while convolving.

For example, if you want to train your neural network to classify whether it is a dog or cat then while applying convolution, kernels are going to extract features from the images like the ear of a dog & tails of a dog much more to get differentiate between dog & cat features that is how convolution work.

As you can see from the above image if you convolve 3 X 3 kernels over 6 x 6 input image size, the size of the image will be reduced by 2 as kernel size is 3 with output as 4 x 4 further applying 3 x 3 on 4 x 4 size will be reduced to 2 x 2 as seen in the above image. But if you will applying 3 x3 now we cannot convolve further as the output image size is 2 x 2 now as mathematically you will get a negative dimension which is not possible.

But if you observe it may happen our network will not consider some of the important features because we end up with just 2 convolutions which are therefore difficult to find that all features are extracted to differentiate between two objects that you are training the neural network with.

Why image size is reduced by 2 only?

We have the formula to calculate the output image size which is:

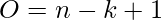
Where O stands for output image size, n is the input image size & k is the kernel size.

If you look at the above example we have input image size as 6 x 6 with kernel size 3 x 3. So, output size after applying the first convolution will be

O = 6 - 3 + 1
O = 4 x 4

Here is one of the reasons why Padding comes into a picture

Why Do We Need padding?

• The main aim of the network is to find the important feature in the image with the help of convolutional layers but it may happen that some features are the corner of the image which the kernel (feature extractor) visit very less number of times due to which there could be a possibility to miss out some of the important information.
• So, padding is the solution where we add extra pixels around the 4 corners of the image which increases the image size by 2 but should be as neutral as possible which means do not alter the original image features in any way to make it complicated for the network to learn further. Also, we can add more layers as now we have a larger image.

We can say for easy understanding that padding helps the kernel (feature extractor) to visit pixels of the image around the corners more times to extract important features for better learning.

If you see the below image showing an illustration of how the kernel is visiting the pixels of the image & it is important that the kernel should visit each pixel at least more than 1 time or 2 times to extract the important features.

Have a look at the above Image while convolving around the image with the kernel as pixels around the corners of the image visited by the kernel very less number of time as compared to the middle part of the pixels.

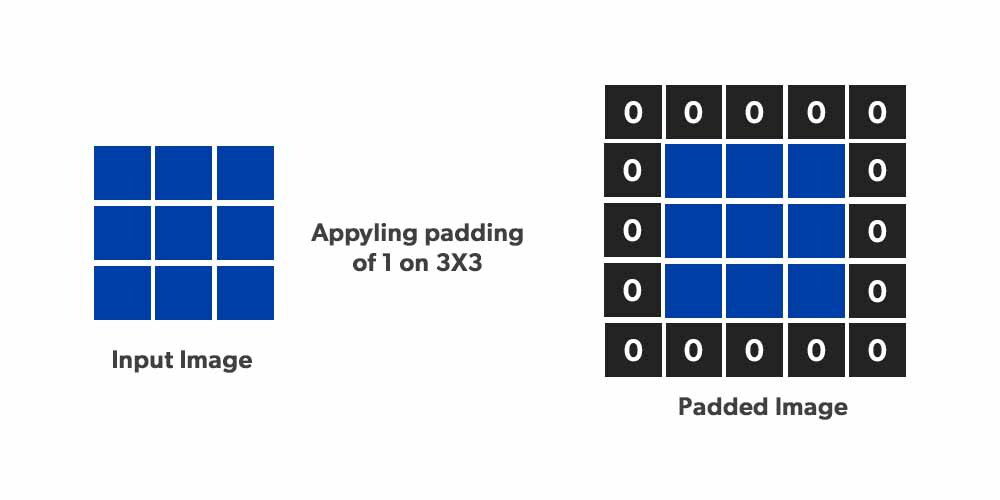
If you can observe from the above picture we have added the padding of Zero around the 4 corners of the image & input image size increased from 6 x 6 to 8 x 8 after applying the first convolution output image size would be 6 x 6 that is what we want as per the question above.

After applying the padding we can observe that there is the possibility of convolving one more time compared to without padding which helps the network to extract more features for better learning at the same time. Even applying the padding helps us to convolve one more time which helps the network to extract more features for better learning at the same time.

If you see the below image & this is how the padded image looks like:

There are two types of padding

• Valid padding where we are not applying padding at all & P=0
• Same padding where output images size should be equal to the input image size due to which we have applied the same padding.

From the above formula we have:

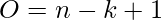
Now, we are adding padding over the 4 sides of an image down, up, right & left side adding zero padding. (NOTE: Here we are not considering strides)

Let’s see a new formula with padding

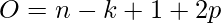
If you see for same padding  O = n (Output image size should be equal to input image size)

So, 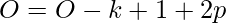 from here we can use simply mathematics in above equation mentioned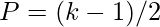 

Why do we always use ODD kernels like 3 x 3, 5 x 5 & so on why not 4 x 4 kernels(even kernels)?

For example, if you want to use a 4 x 4 kernel then what will be the padding you have to use?

You can use the above formula p =( k – 1)/2

We have kernel = 4 x 4

p= 4 -1/2  =  3/2 = 1.5

Which means you have to add 1.5 pixels around 4 corners of the image to apply padding, which in turn is not possible because we can’t add 1.5 pixels instead we can only add the pixels in whole numbers like 1,2,3,4,5,6 & 7 so on pixels around the corners of the image.

This is one of the reasons why kernels are always an odd number so that we can add a whole number of pixels around the image to extract more features as adding 1.5 pixels around doesn’t make any sense & is difficult to add at the same time.

Why do we always use padding = 1 & what do we mean by saying that you are using padding of 1. In all the standard networks you notice that the padding used is always 1, as simply while we are padding we are adding some information by ourselves and it not a good idea to interfere with the network that a lot as the best features learned by the network is the self-learned once and also will be increasing the input size a lot and make the model heavy.

Why “zero-padding”?

Now one of the questions that arise in our mind is why do people always use zero(0) padding blindly just following what we have read in blogs or any course. So, now we understand how padding is working, and how it is important for a neural network. But one question always comes to our head, why only 0 padding? Why can’t we use 1-padding or any number?

When we normalize an image, the pixel range goes from 0 to 1, and if it hasn’t been normalized then the pixel range will be from 0 to 255.

If we consider both cases, we can see 0 is the minimum number. So, using 0 becomes a more generic way of doing this. Also, it makes sense computationally since we are considering the minimum number among those pixels.

But it is not always 0, Consider a case where we have values ranging from -0.3 to 0.3, in this case, the minimum number is -0.3, and if we use the padding of 0 around it, it would be Gray instead of black. The same case comes when we have an activation function like tanh, which ranges the values from -1 to 1, in this case, the minimum value is -1., so we would be using (-1) padding instead of 0 paddings, for adding black pixels around it. If we use 0 paddings, then it would be a gray color boundary instead of black color.

But Here, is a problem, it is not always possible where we can calculate what will happen to inactivation values, so we look for a neutral value that can satisfy most of the cases without problem, and this is where 0 padding saves us. If we even consider the above-mentioned two ranges, we can see, the use of 0 padding would give a gray boundary instead of black, which is not a huge loss. We can also call these cases, “The Minimum Padding Case”, where we are considering the minimum value among activation maps.

Most of the time, we use relu in between layers, so in the case of relu, 0 becomes the minimum value and that is why it is so popular and generic.

Do we need to add padding in every layer?

Let’s understand this with the help of an example, lets the MNIST digit recognizer dataset

Here are some sample images from the MNIST dataset. Above we discussed two main reasons to use padding:

• Shrinking Output after convolution, so we can add more layers to extract more features
• Add to save the loss of information around the edges

You can see that the numbers in the dataset are not around the edges, they are mainly at the center. That means there may be very little information around the edges. So, the main reason to add padding, in this case, is to add more layers. But also MNIST does not require that many layers. You may add padding in the initial layers but in all the layers it would be of much use, you will be just making your model heavier.

In conclusion, it depends on the datasets and the problem statement, which layers would require padding.