What is Mapping Cardinalities in ER Diagrams

In a Database Management System (DBMS), mapping cardinalities explains how entities (tables) in a database schema relate to one another. They provide the number of instances of one entity that can be linked to the number of instances of another entity via a certain kind of relationship, such as many-to-many, one-to-one, or many-to-many. Designing exact links between tables, preserving data integrity, and simulating actual business operations in a database all depend on the mapping of cardinalities. They are a cornerstone of database design’s entity-relationship paradigm.
Whenever an attribute of one entity type refers to another entity type, then some relationship exists between them. 

Example:

Example of Mapping Cardinalities

• The attribute Manager of the department refers to an employee who manages the department.
• In the ER model, these references are represented as relationships.

Relationship

The relationship in the ER model is represented using a diamond-shaped box.

Example:

Example of Relationship in DBMS

‘Buys’ is a relationship between customer entity and products. This relationship can be read as ‘A customer buys a product/products.

Therefore, a relationship is a way to connect multiple entities.

• When a  customer buys a product, there is a timestamp associated with it, so the attribute “Time” will be an attribute of ‘Buys’.
• All the database concepts can be easily understood from the concepts of sets and relations.
• According to the Set-theoretic perspective, it will be represented as

Example

By interpreting this, we can understand that many customers can buy the same type of product and many products can be bought by many customers. And there are some products which are not bought by any customer and there are some customers who do not buy any product.

According to the Relation/table perspective or relational model:
It can be represented as  

Many to many Relationship

As the relationship is many to many(M: N) between customer and product, therefore we require separate tables/ relations for ‘buys’. 
In buys relation, Cust_id and Prod_id are the foreign key to the customer and product. 

Mapping Cardinality/Cardinality Ratio

Mapping cardinality is the maximum number of relationship instances in which an entity can participate.

Example:

Entity type employee is related to department entity type by works_for relationship

Mathematically, here (e1, e2,e3…) are instances of an entity set Employee and (d1,d2, d3 ….) are the instances of entity type department and (r1, r2, r3 …) are relationship instances of relationship type.

Each instance r_i(where i = 1,2,3,….) in R, is an association of entities, and the association includes exactly one entity from each participating entity type. Each such relationship instance, r_i represents that the entities participating in ri are related in some way by any constraint/condition provided by the user to a designer.

• In works_for binary relationship type Department: Employee is of cardinality(N:1), this means each department can be related to any number of employees but an employee can be related to(works for) only one department.
• The possible cardinality ratios of binary relationship types are (1:1, 1:N, N:1, N:M).

Participation or existence constraint:
It represents the minimum number of relationship instances that each entity can participate in and it is also called the minimum cardinality constraint. There are two types of participation constraints, which are total and partial.

Example:

• In the above example, if the company policy is that every employee should work for a department. Then all the employees in the employee entity set must be related to the department by a works_for relationship. Therefore, the participation of the employee entity type is total in the relationship type. The total participation is also called existence dependency.
• And if there is a constraint that a new department need not have employees, then some entity in the employee entity set is not related to the department entity by works_for relationship. Therefore, the participation of employee entity in this relationship(works_for) is partial.
• In the ER diagram, the total participation is represented using a double line connecting the participating entity type to the relationship, and a single line is used for partial participation.

The cardinality ratio and participation constraint together is called structural constraint of the relationship type.
All possible cardinality ratios for binary relationships are explained below with an example.

1. One to one relationship (1:1)

It is represented using an arrow(⇢,⇠)(There can be many notations possible for the ER diagram).
Example:

One to One relationship

In this ER diagram, both entities customer and driving license having an arrow which means the entity Customer is participating in the relation “has a” in a one-to-one fashion. It could be read as ‘Each customer has exactly one driving license and every driving license is associated with exactly one customer.

The set-theoretic perspective of the ER diagram is

ER diagram

There may be customers who do not have a credit card, but every credit card is associated with exactly one customer. Therefore, the entity customer has total participation in a relation.

2. One to many relationship (1:M)

Example:

one to many relationship

This relationship is one to many because “There are some employees who manage more than one team while there is only one manager to manage a team”.
The set-theoretic perspective of the ER diagram is:

ER diagram

3. Many to one relationship (M:1)

Example:

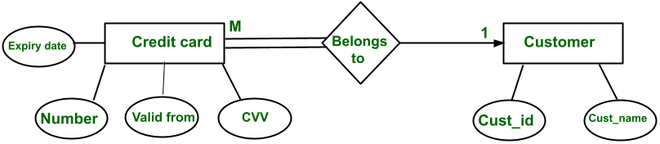
Many to one realtionship

It is related to a one-to-many relationship but the difference is due to perspective.
Any number of credit cards can belong to a customer and there might be some customers who do not have any credit card, but every credit card in a system has to be associated with an employee(i.e. total participation). While a single credit card can not belong to multiple customers.
The set-theoretic perspective of the ER diagram is:

ER diagram

4. Many to many relationship (M:N)

Example:
A customer can buy any number of products and a product can be bought by many customers. 

Many to many Relationship

The set-theoretic perspective of the ER diagram is:

ER diagram

Any of the four cardinalities of a binary relationship can have both sides partial, both total, and one partial, and one total participation, depending on the constraints specified by user requirements.

Conclusion

The number of instances of one entity that can be connected to the number of instances of another object is specified by mapping cardinalities in a database schema, which explain how entities (tables) link to one another. This kind of interaction is essential for preserving data integrity and precisely simulating processes in the real world within a database. By expressing cardinalities as one-to-one, one-to-many, and many-to-many, mapping cardinalities aids in defining the guidelines for data interactions in database management systems (DBMSs).