What is 2i equal to?
Last Updated :
30 Nov, 2021
Complex numbers are the combination of real values and imaginary values. They are expressed in the form of x + iy where x and y are real numbers and i is the imaginary part also called iota. It is often represented by z. The value ‘x’ is called the real part, denoted by Re(z) and the value ‘y’ is called the imaginary part which is denoted by Im(z). In complex numbers, one part is purely real and the other part is purely imaginary.
Real and Imaginary numbers
Real Numbers are those numbers whose square gives a positive result. They can be positive, negative, integers, rational, irrational, etc. They can be represented on a number line. It is represented by Re().
Imaginary Numbers are those numbers whose square gives a negative value. They cannot be represented on a number line. They are denoted by Im(). The imaginary numbers are of the form ‘bi’ where i is the iota and b is the real number.
Example: z = 1 + 4i
Here in the above example, it is of the form a + ib where a = 1 and b = 4 which are real numbers.
Re(z) = 1
Im(z) = 4
More About Iota
An imaginary number is denoted by iota ‘i’. The ‘i’ used in complex numbers is known as iota. It is used to find the square root of negative numbers.
Value of i = √(-1)
- If the square operation of i is performed,
i2 = i.i = -1
- If the cubic operation of i is performed,
i3 = i.i.i = -i
- And finally, if the fourth power of iota is calculated,
i4 = (-1)(-1) = 1
Note: Since 0 can be represented by the form 0 + 0i it is real as well as complex.
Operations on Complex numbers
In complex numbers, can perform addition, subtraction, multiplication, division, and conjugation. The operations are done separately for the real part and imaginary parts. In division, rationalize the denominator and perform the operation accordingly.
- Addition: Perform addition of complex numbers by adding the real parts and imaginary parts separately. Let’s assume two complex numbers a + ib and c + id. The following operation is as follows,
a + ib + c + id = (a + c) + i(b + d)
- Subtraction: In addition, perform the subtraction of complex numbers by subtracting the real and imaginary parts separately. Let’s assume two complex numbers a + ib and c + id. The following operation is as follows:
a + ib – (c + id ) = (a – c) + i( b – d)
- Multiplication: When two complex numbers say z1 and z2 are multiplied, the real part of z1 is multiplied with both the real and imaginary parts of z2 and similarly, it is done for the imaginary part of z1. Let us assume two complex numbers a + ib and c + id. The following operation is as follows:
(a + ib) × (c + id) = ( ac – bd) + i(ad + bc)
- Conjugate: Let’s take a complex number z. The conjugate of z is found by changing the sign of the imaginary part of the complex number that means changing of + to – and – to +. Let’s assume one complex number a + ib. The following operation is as follows:
conjugate(a + ib) = (a – ib)
- Division: When the division of two complex numbers z1 and z2 are performed we multiply the denominator z2 by its conjugate and perform the operation accordingly. Let us assume two complex numbers a + ib and c + id. The following operation is as follows.:
(a + ib)/(c + id) = {(a + ib) (c – id)}/(c2 + d2)
The absolute value of a complex number
The absolute value is the modulus of any number be it complex or real. Suppose z = x + iy is a complex number. The mod of z is |z| = √x2 + y2. The absolute value is always positive irrespective of the sign of the complex number. It is just a magnitude.
What is 2i equal to?
Answer:
So now 2i can be expressed in the form of 0 + 2i
The absolute value of 2i is
|z| = √(0)2 + (2) 2 = √4 = 2
Similar Problems
Question 1: Find the value of -4i?
Solution:
Represent 4i in the form 0 – 4i
The absolute value is 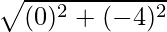 which is 4.
which is 4.
Question 2: Find value of 2 + i?
Solution:
The absolute value is 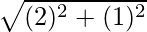 = √5
= √5
Question 3: The absolute value of -5 + bi is 13. Find all the values of b.
Solution:
As known, the absolute value of a complex number is calculated by using the formula √x2 + y2 .
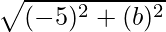 = 13
= 13
=> (-5)2 + b2 = 169 [Squaring both sides]
=> b2 = 169 – 25
=> b2 = 144
=>b = +12 or -12
The values of b are 12 or -12
Share your thoughts in the comments
Please Login to comment...