What does ‘i’ equals to in algebra?
Last Updated :
03 Jan, 2024
The combination of Real and Imaginary Numbers is called a Complex Number. It is represented by ‘Z’. Complex numbers have many applications like they are particularly valuable in hardware, optics, and quantum hypothesis for portraying waves. Also, Fourier changes utilize complex numbers.
Mathematically, a Complex number is represented as Z = a + ib, where a is the Real part and b is the imaginary part. Here, i is the imaginary number and it is called “iota”. For example, 5 + 3i, where 5 is the real number and 3i is the imaginary number. Consequently, a complex number is a simple representation of the expansion of two numbers, i.e. real number and an imaginary number. One piece of it is simply real (Re) and the other part is absolutely imaginary (Img).
There are various forms of complex numbers mainly 3 types, Rectangular form: z = a + ib, Polar form: z = r(cosθ + isinθ), and Exponential form: z = re (iθ) where, θ is the angle (in radians) between the positive real axis and the line segment that connects the origin and z.
Real Numbers
Any number which can be plotted on a number line is called a Real number. Every one of the negative and positive numbers, decimal and partial numbers are called real numbers. They do not include any imaginary value. They are very often used in practical life for performing various algebraic operations, solving simple and long equations, geometry, etc. Real numbers are denoted by ‘R’. It consists of,
- Rational numbers: A rational number is a real number which is in the form of fraction p/q where q is not equal to 0. It is denoted by ‘Q‘. It consists of terminating decimals and non-terminating recurring decimals and thus cannot be represented in fractional form. Example of rational number- 0.53, 4, 5.768, 3/2, 1.2222222… Also, rational numbers contain perfect squares like 4, 9, 16, 25, 49, etc.
- Irrational numbers: An irrational number is a real number that cannot be represented in the form of a fraction or When any number cannot be expressed in form of a quotient when dividing two numbers, it is referred to as rational numbers denoted by ‘R – Q‘. It consists of non-terminating non-recurring decimals. Example of irrational numbers: √(2) = 1.41421356…, √(5) = 2.23606…, π.

Representation of Real Numbers on Number Line
Imaginary Numbers (i)
It is defined as the square root of negative natural numbers or we can say any number which yields a negative number after squaring. They combine with real numbers to form complex numbers and have a huge impact on number theory and geometry. They also play an important role in engineering and practical life for example it is used in electrical circuits to represent various physical quantities and circuits and solve some complex quadratic equation in modern physics. Example: √(-2), √(-7), etc.
What does i equal in algebra?
Answer:
It was invented by mathematicians back then when while having problems finding the roots of some cubic equations and they noted the fact that some numbers that it is said imaginary today cannot be represented on the x-axis, so why not use the y-axis to represent them and thus gave rise to the concept of square roots of negative number i.e. imaginary numbers.
It is denoted by ‘i’, where the value of i is considered as √(-1). Any real number when multiplied by an imaginary number will result in an imaginary number. For example 5 × √(-1) = √(-5) or 5i. Imaginary numbers, as its name suggests are not actually imaginary. They do exist. Let us take an example:
Let suppose solving a quadratic equation x2 = -4. In the above equation, one can’t find the root of -4, which implies that there are no real roots i.e the parabola does not cut the x-axis as shown in the diagram.
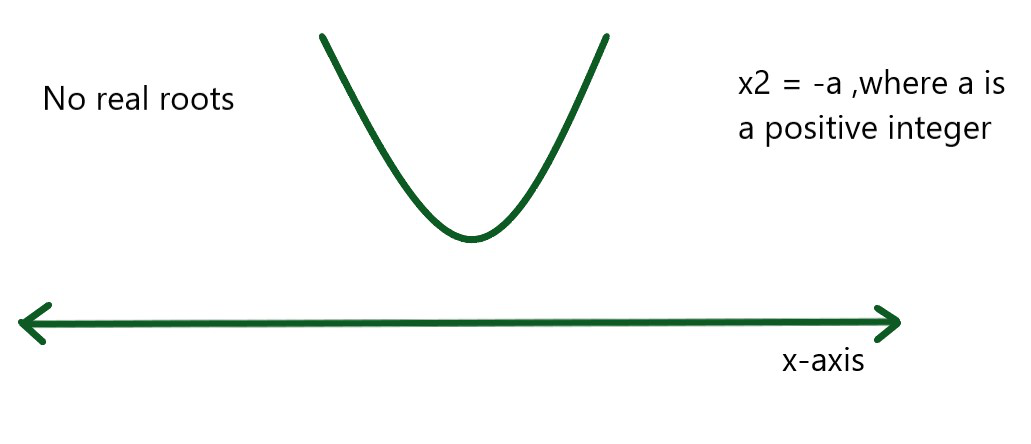
Write the above equation as x2 = -1 × 4. Now, we know the square root of 4 is +2 and -2.
But the square roots of -1 is not known, so mathematicians invented a new number as √(-1) and named it ‘i’ (standing for imaginary number) Now one can solve the above equation by assuming √(-1) as i and get the respective roots as +2i and -2i.
Evolution of Imaginary Numbers
Imaginary numbers were also found like all the other numbers in the number system as their need arises. First natural numbers were found in the early human civilization which are invented to perform normal counting. Then ‘0’ was invented to represent nothing, combining with natural are called whole numbers. After that negative numbers were invented which also have physical significance, for example, representing debt or going in the opposite direction.
Combining whole numbers and negative numbers are called integers. Then came rational Numbers, used to calculate a part or fraction of something. Then after some time, irrational numbers were found by greek mathematicians while finding the hypotenuse of the right-angle triangle of base and size both 1unit and finally, the imaginary numbers were found when the mathematicians are unable to solve some quadratic equations as discussed in the above topic.
Real-life Example of Imaginary number
Suppose a man is moving in a particular direction with a velocity X. After some time, due to some reason its direction gets reversed and thus the velocity becomes ‘-X’. This signifies that if the man is rotating by 180 degrees, then his velocity is been multiplied by ‘-1’. Now assume if the man needs to change his direction on the path perpendicular to the original path then he needs to rotate only half the rotation he needs to do while going in the opposite direction. Let’s represent this rotation by r.
Considering the above example, we can say that r . r = -1. (Since two 90° rotations = one 180° rotation). After taking a 90° turn, the new velocity of the man will become X.r, where r = √(-1) ( imaginary number).

Representation of Imaginary Numbers
Sample Problems
Question 1: Which of the following among the given number are imaginary numbers?
- -1
- √7
- 2√-1
- 3i
- √-4
- √(-1)2
Solution:
3, 4, 5, are imaginary numbers as they all have negative numbers in square root.
Question 2: Find out the values of the following terms,
- i2
- i3
- i4
- i5
- i6
- i271
- i74
- i-1
Solution:
- i2 = -1
- i3 = i
- i4 = 1
- i5 = i
- i6 = -1
- i271 = i4 x 67.i3 = 1 × i = i
- i74 = i4 x 18.i2 = 1 × -1 = -1
- i-1 = 1/i (multiplying both numerator and denominator by i => i/i2 = i/-1 = -i)
Question 3: Write the imaginary part of the given complex numbers.
- 4 + 3√-1
- i2 + i
- √7 + 6i
- -4 + 2i
Solution:
- 3
- 1
- 6
- 2
Question 4: Reduce the following imaginary numbers as the multiple of i or √(-1).
- √(-9)
- 5√(-3)
- 6i2
- 3√(-4)3
Solution:
- √(-9) = 3√-1 = 3i
- 5√(-3) = 5√3√-1 = 5√3i
- 6i3 = 6i ( since i.i.i = i)
- 3√(-2)3 = 3 × 2√2√-1 = 6√2i
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...