An angle is a form of geometrical shape constructed by joining two rays to each other at their end points. The two lines joined together are called the arms of the angle and the measure of the opening between them is the value of the angle between these two lines.
In this article, we will learn about the definition and parts of angles in Geometry, their representation, examples, and types like acute angle, right angle, obtuse angle, etc. along with FAQs.
Angle Definition
An Angle is a shape or space formed at the meeting point of two intersecting rays.∫
An angle is formed when two rays are joined together at a common point. The two lines are called ‘Arms of the Angle’ and the common point of the meeting is called a ‘Vertex’.
Symbol of an Angle
Angle is represented by the symbol “∠”
Representation of an Angle
While writing an angle ∠ is used along with the points. The common point is written in between the two other points. For Example, if we have ∠AOB, it means O is the common point at which two rays OA and OB are meeting and an angle is formed.
 Representation of an Angle
Representation of an Angle
Parts of an Angle
An angle consists of the following parts :
- Arms of the Angle
- Vertex of the angle
- Initial Side
- Terminal Side
The image shown below shows the parts of an angle.
 Parts of an Angle
Parts of an Angle
Arms of an Angle
The two rays that joint together to form the angles are called the arms of the angle. In the image added below, OP and OQ are the arms of the angle. The space between these two arms is the measure of the angle.
Vertex of an angle
The endpoint of the two arms of the angles is called the vertex of the angle. It is the point where the arms of the angle meet. In the above image added O is the vertex of the angle.
Types of Angles
There are different types of angles judged on the basis of four different parameters. They are mentioned as follows:
- On the Basis of Measurement
- On the Basis of Rotation
- On the Basis of Pair
- On the Basis of Intersection by Transversal
Types of Angles Based on Measurement
There are six types of angles on the basis of measurement. They are:
Learn More, 7 Types of Angles
Acute Angle
The angle that measures less than 90° is the Acute Angle. The degree always measures between 0 and 90.
Acute angles measure positive when the rotation is anticlockwise and negative when the rotation of the angle is clockwise.
 Acute Angle
Acute Angle
In the figure, O is the vertex of the angle, and OA and OB are two intersecting rays that meet at point O forming an angle less than 90°. Hence, ∠AOB is an acute angle.
Right Angle
The angle that exactly measures 90° is called a Right Angle.
It is also considered as a half straight angle as half of 180° makes a right angle. The value of the angle may be positive or negative on the basis of the rotation of the angle.
 Right Angle
Right Angle
In the figure, O is the vertex of the angle, and OA and OB are two intersecting rays that meet at point O forming an angle of exactly 90°. Hence, ∠AOB is a right angle. Also when two rays meet to form a 90° angle there are called Perpendicular to each other. Here OA and OB are perpendicular to each other.
Obtuse Angle
The angle that measures more than 90° and less than 180° is called an Obtuse Angle. The degree always lies between 90° and 180°.
The value of the obtuse angle will be positive if the rotation is anticlockwise and negative if the rotation is clockwise.
 Obtuse Angle
Obtuse Angle
In the figure, O is the vertex of the angle, and OA and OB are two intersecting rays that meet at point O forming an angle of more than 90°. Hence, ∠AOB is an obtuse angle.
Straight Angle
The angle that measures exactly 180° is a Straight Angle. It is called Straight Angle because when two rays make 180° between them then they are in a straight line.
 Straight Angle
Straight Angle
In the figure, of a straight angle, we can observe that O is the meeting point of two arms, called the vertex and OA and OB are two sides of the angle.
Reflex Angle
The angle that measures more than 180° and less than 360° is called a Reflex Angle. The degree always lies between 180° and 360°.
 Reflex Angle
Reflex Angle
In the figure, O is the vertex of the angle, and OA and OB are two intersecting rays that meet at point O forming an angle of more than 180°. Hence, ∠AOB is a reflex angle.
Complete Angle
The angle whose measurement is 360° is called a Complete Angle. It happens when you make a complete turnaround and reach the initial point then in this case the angle is Complete Angle.
 Complete Angle
Complete Angle
Let’s now study angle on the basis of Rotation
Types of Angles Based on Rotation
There are two types of angles on the basis of Rotation. They are listed as follows:
- Positive Angle
- Negative Angle
Positive Angle
The angle that moves anticlockwise from its base and is drawn from the point (x, y) which is its origin is called a positive angle.
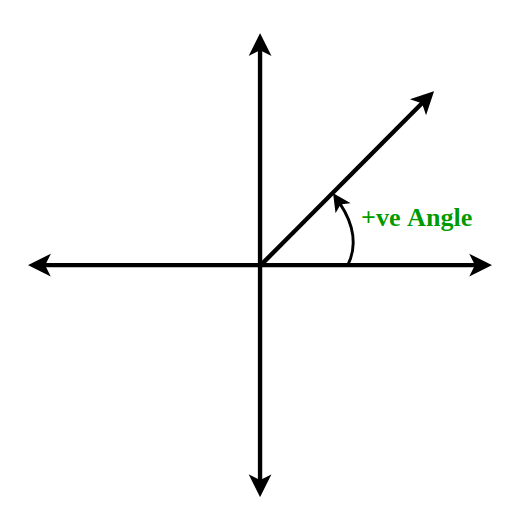 Positive Angle
Positive Angle
Negative Angle
The angle that moves clockwise from its base and is drawn from the point (-x, -y) which is its origin is a negative angle.
 Negative Angle
Negative Angle
Now we will study the angles on the basis of pair.
Types of Angles in Pair
There are five types of angles on the basis of pairs. They are :
- Complementary Angles
- Supplementary Angles
- Adjacent Angles
- Linear Pair
- Vertically Opposite Angles
Now let’s learn each of these angles in pair in detail.
Complementary Angles
If the summation of two angles measures 90° then, the angles are said to be Complementary Angles and each angle is called a complement of the other.
The two angles combining together do not require to be adjacent or similar. It can be any two types of angles measuring 90° after addition. For Example, 70 and 20 are complementary angles.
Supplementary Angles
If the summation of two angles measures 180°, the angles are said to be Supplementary Angle. Each Angle is called a Supplement of the other.
For Example, 150° and 30° are Supplementary Angles.
Adjacent Angles
Two angles are said to be adjacent if they have a common vertex, a common arm, and the rest two arms lie on the alternate side of the common arm. Angle AOC and Angle BOC are Adjacent Angles
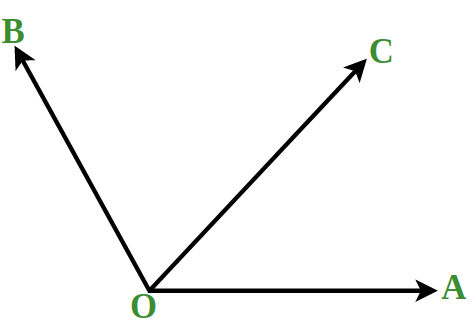
∠AOC and ∠BOC are here adjacent because they have a common point O, a common vertex OC and rest two arms OA and OB lie on the alternate side of the common arm.
Linear Pair
When the sum of two adjacent angles is 180° then they are called a Linear Pair.
As the name suggests the pair of angles result in a straight line.
Remember that there is one difference between Supplementary Angle and Linear Pair. For a Linear Pair, the two angles must be adjacent while there is no such condition for Supplementary Angles. For Supplementary Angles, only the sum of the angles should be 180° doesn’t matter if they are adjacent or not. Here ∠AOC and ∠BOC are linear pairs as AOB is a straight line.

Vertically Opposite Angles.
When two lines intersect each other at a common point then the pair of angles in front of each other are called Vertically Opposite Angles.
- In the below figure, AB and CD are two lines that intersect each other at O, then pairs of Vertically Opposite Angles are (∠AOC, ∠BOD) and (∠AOD, ∠BOC).
- It should be noted that a pair of vertically opposite angles are equal i.e. ∠AOC = ∠BOD) and ∠AOD = ∠BOC).
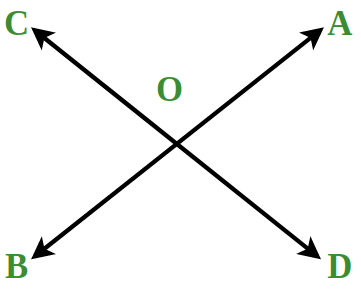
Let’s now discuss the final category of angles i.e. Angles formed by the Transversal and Parallel Lines
There are four types of angles formed by transversal and parallel lines. They are :
Now let’s learn about these in detail.
Corresponding Angles
The Angles that are present at similar positions and on the same side of the transversal are Corresponding Angles. Corresponding Angles are the same in measurement.
In the figure below, ∠AOL and ∠CPM are corresponding angles placed at similar positions one at the exterior and the other at the interior part.
Alternate Interior Angles
The angles which are present on opposite sides of the transversal is the alternative interior angle. They are present at the inner side of the Z formed in the figure. The pair of Alternate Interior angles are equal to each other.
In the figure below, ∠AOT and ∠OTR are alternate interior angles placed interiorly alternate to each other. Similarly, ∠BOT and ∠OTQ are also Alternate Interior Angles.
Alternative Exterior Angles
The angles present on opposite sides of the transversal but externally are the alternative exterior angle. They are spotted at the exterior part of Z and both the angles measure the same.
In the figure below, (∠AOL, ∠DPM) and (∠BOL, ∠CPM) are the pair of Alternate Exterior Angles.
Consecutive Interior Angles
When two interior angles of the same side of the transversal are placed consecutively i.e. just after the other then they are called Consecutive Interior Angles. The sum of the pair of Consecutive Interior Angles is 180°.
In the below figure pair of Consecutive Interior Angles are (∠BOP, ∠CPO) and (∠AOP, ∠OPD).

Interior and Exterior Angles
Interior and exterior angles depends on the region of the angle where they are made. Let’s learn about interior and exterior angles below.
Interior Angle
The angles that are formed inside any shape are called the Interior angles. For Example, angle inside a triangle, quadrilateral etc.
Exterior Angle
The angle that are formed outside any shape are called the exterior angles.
Suppose we take a triangle ABC then and extend the line BC to D then in that figure we can easily mark the interior and exterior angles.
Here, in the above figure, ∠ABC, ∠BCA, and ∠CAB are interior angles and ∠ACD is the exterior angle.
Measurement of Angles
- The angle can be measured in ‘Degree’ or ‘Radian’. In the case of Degrees, the measurement goes from 0° to 360° while in the case of Radian measurement goes from 0 to π.
- The smaller units of angle are minutes and seconds. Minute is represented by a single apostrophe(‘) while second is represented by a double apostrophe(”). We should remember below mentioned relations among various units of angles:
- π = 180°
- 1° = 60′
- 1′ = 60”
Angle in Degree
To convert the Angle from Degree to Median, we should multiply the given angle(in degrees) by π/180. Let’s see one example
Example: Convert 90° to Radian
Solution: 90° × π/180 = π/2
Angle in Radian
To convert the Angle from Radian to Degree we should multiply the given angle(in radians) by 180/π. Let’s see one example
Example: Convert π/2 to Degrees.
Solution: (π/2) × (180/π) = 90°
Learn more, Degrees to Radians
How to Measure an Angle
An angle can be measured easily by using a protector or compass. In general, we use the protector to measure the angles. Follow the steps added below to measure the angle,
- Step 1: Place the protector above one of the arms of the angle.
- Step 2: Measure the value in the anticlockwise direction or clockwise direction depending on the opening of the angle then mark the value where the angle’s arms coincide with the value in the protector.
- Step 3: The reading obtained in the protector is the required measure of the angle.
Steps to Construct an Angle
An angle can be easily constructed using the proctor or compass. To construct an angle using the protractor we follow the steps added below,
Step 1: Draw a ray OA of any length that is parallel to horizontal edge of page.
Step 2: Place the protractor on the ray OA such that O is at the centre of the protractor. And OA is at the right side of the protractor.
Step 3: Mark the point from the right side of the protractor at the angle which we want to construct suppose we have to construct an angle of 60°(mark the point as P)
Step 4: Join OP ∠AOP is the required angle.
Some Important Results on Angles
There are some results on angles that are generally used while solving problems of geometry. We have mentioned some of them down below.
- Angle on any side of a straight line is 180°
- Angle around a point is 360°
- Vertically Opposite Angles are equal
- Alternate Interior Angles are equal
- Corresponding Angles are equal.
- Sum of all three angles in a triangle is 180°
- Sum of all four angles in a quadrilateral is 360°
- Linear Pair always sum to 180° and are formed on either side of a straight line.
- Complementary Angles sum to 90°
- Supplementary Angles sum to 180°
Read More,
Solved Examples on Angles
Here we have provided you with a few solved examples to help you understand the concept of angles very clearly.
Example 1: Find the complementary angle of ∠A = 48o.
Solution:
Given angle,
∠A = 48o
Complement of any Angle = 90o – Angle
Complement of ∠A = 90o – 48o
Complement of ∠A = 42o
Thus, the complement of ∠A is 42o
Example 2: Find the supplemenatry angle of ∠A = 48o.
Solution:
Given angle,
∠A = 48o
Supplement of any Angle = 180o – Angle
Supplement of ∠A = 180o – 48o
Supplement of ∠A = 132o
Thus, the complement of ∠A is 42o
Example 3: Find the supplementary angle of ∠A = 98o.
Solution:
Given angle,
∠A = 98o
Supplement of any Angle = 180o – Angle
Complement of ∠A = 180o – 98o
Complement of ∠A = 82o
Thus, the complement of ∠A is 82o
Example 4: Classify the angles into different categories,
- ∠A = 12o
- ∠B = 172o
- ∠C = 232o
- ∠D = 180o
Solution:
(1) ∠A = 12o
As the measure of ∠A is less than 90o, thus it is an acute angle.
∠B = 172o
As the measure of ∠B is greater than 90o, thus it is an obtuse angle.
∠C = 232o
As the measure of ∠C is greater than 180o, thus it is a reflex angle.
∠D = 180o
As the measure of ∠D is equal to 180o, thus it is a straight angle.
Practice Problems on Angles
Mentioned below are a few practice problems on angles for you to solve on your own:
1. Find the Supplementary Angle of ∠A = 82°
2. Find the Supplement of Angle ∠A = 108°
3. Find the Complementary Angle of ∠A = 45°
4. Find the Complement of Angle ∠A = 60°
Angles Definition, Types and Examples – FAQs
1. What are the different types of Angles?
There are mainly six types of angles. They are listed as follows:
- Acute angle: Measures less than 90°
- Right Angle: Measures exactly 90°
- Obtuse angle: Measures more than 90° and less than 180°
- Straight angle: Measures exactly 180°
- Reflex angle: Measures more than 180° and less than 360°
- Complete Angle: Measures Exactly 360°
2. What are Angles?
An angle is a form of geometrical shape, that is constructed by joining two rays to each other at their end-points.
3. What are Different Types of Angles formed by Parallel Lines and Transversal?
The different types of angles formed by Parallel lines and Transversal are Corresponding Angle, Alternate Interior Angle, Alternate Exterior Angle and Consecutive Interior Angles.
4. What is a Linear Pair of angles?
When the sum of two adjacent angles is 180° then the pair of angles are called Linear Pair.
5. What are Complementary Angles?
Two angles whose sum is 90° are called Complementary Angles.
6. What are Supplementary Angles?
Two angles whose sum is 180° are called Supplementary Angles.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...