Whale Optimization Algorithm (WOA)
Last Updated :
12 Apr, 2021
The step-by-step procedure to obtain an optimum value (maximum or minimum) of an objective function is called an Optimization Algorithm.
Meta-heuristic optimization algorithms are becoming more and more popular in engineering applications because they:
- rely on rather simple concepts and are easy to implement
- do not require gradient information
- can bypass local optima
- can be utilized in a wide range of problems covering different disciplines.
Many scholars and researchers have developed several metaheuristics to address complex/unsolved optimization problems. Example: Particle Swarm Optimization, Grey wolf optimization, Ant colony Optimization, Genetic Algorithms, Cuckoo search algorithm etc.
This article aims to introduce a novel meta-heuristic optimization technique called as Whale Optimization algorithm (WOA)
Inspiration of the algorithm:
Whale optimization algorithm (WOA): A nature inspired meta-heuristic optimization algorithm which mimics the hunting behaviour of humpback whales. The algorithm is inspired by the bubble-net hunting strategy
Foraging behavior of Humpback whales is called bubble-net feeding method. Humpback whales prefer to hunt school of krill or small fishes close to the surface. It has been observed that this foraging is done by creating distinctive bubbles along a circle or ‘9’-shaped path as shown in Fig. 1.
Two maneuvers associated with bubble net feeding are ‘upward-spirals’ and ‘double-loops’.
- In ‘upward-spirals’ maneuver humpback whales dive around 12 m down and then start to create bubble in a spiral shape around the prey and swim up toward the surface.
- ‘double-loops’ maneuver includes three different stages: coral loop, lobtail, and capture loop

Figure 1: Bubble-net feeding behaviour of humpback whales.
Mathematical Model
Bubble-net feeding is a unique behaviour that can only be observed in humpback whales. In whale optimization algorithm (WOA) the spiral bubble-net feeding maneuver is mathematically modeled in order to perform optimization
- WOA simulated hunting behaviour with random or the best search agent to chase the prey
- WOA uses a spiral to simulate bubble-net attacking mechanism of humpback whales
Encircling Prey
Current best candidate solution is assumed to be closes to target prey and other solutions update their position towards the best agent

(1)
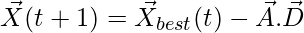
(2)
Where t indicates the current iteration, 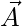 and
and 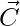 are coefficient vectors,
are coefficient vectors, 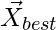 is the position vector of the best solution, and
is the position vector of the best solution, and 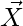 indicates the position vector of a grey wolf
indicates the position vector of a grey wolf
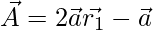
(3)

(4)
Where 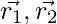 are random vectors in [0, 1].
are random vectors in [0, 1].
Bubble-net attacking method (exploitation phase)
In order to mathematically model the bubble-net behaviour of humpback whales, two approaches are designed as follows
- 1. Shrinking encircling mechanism
- This behaviour is achieved by decreasing the value of
 . a is decreased from 2 to 0 over the course of iterations.
. a is decreased from 2 to 0 over the course of iterations.
- 2. Spiral updating position
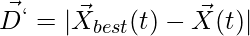
 (5)
(5)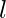 is a random number in [-1, 1]
is a random number in [-1, 1]
Search for prey:
Humpback whales search randomly according to the position of each other
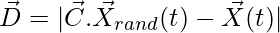
(6)

(7)
Algorithm
Step1: Initialize the whales population  Step2: Calculate fitness of each search agent
Step2: Calculate fitness of each search agent
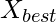 = the best search agent
Step3: while( t < maximum number of iterations )
for each search agent:
Update
= the best search agent
Step3: while( t < maximum number of iterations )
for each search agent:
Update 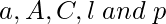 if(p<0.5):
if(|A|<1):
Update current agent by eq. (1)
else:
Select a random agent
if(p<0.5):
if(|A|<1):
Update current agent by eq. (1)
else:
Select a random agent 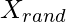 update current agent by eq (7)
else:
update search agent by eq (5)
end-for
Check if any search agent goes beyond the search space and amend it
Calculate fitness of each search agent
Update
update current agent by eq (7)
else:
update search agent by eq (5)
end-for
Check if any search agent goes beyond the search space and amend it
Calculate fitness of each search agent
Update 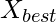 if there is a better solution
t = t+1
end-while
Step4: return
if there is a better solution
t = t+1
end-while
Step4: return 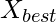
References:
https://www.sciencedirect.com/science/article/pii/S0965997816300163
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...