Weighted Product Method – Multi Criteria Decision Making
Last Updated :
04 Jan, 2022
Weighted Product Method is a multi-criterion decision-making method in which there will be multiple alternatives and we have to determine the best alternative based on multiple criteria. There are other methods available including the Weighted Sum Method (WSM), Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS), VIKOR, MOORA, GTMA, etc. Let’s understand how the Weighted Product Method works with an example.
Consider a case where we have to select the best candidate among 5 candidates who are appearing for an interview. Table 1 consists of the details of 5 students which includes their CGPA, the salary that they are expecting per month, their scores in the technical exam and the grades achieved by them in the aptitude test.
Table 1: Sample Data Set
| Attribute |
CGPA |
Expected Stipend |
Technical Exam Score |
Aptitude Test Grade |
| Student 1 |
9 |
12000 |
72 |
B1 |
| Student 2 |
7.6 |
8500 |
68 |
B1 |
| Student 3 |
8.2 |
9500 |
63 |
B2 |
| Student 4 |
8.5 |
10000 |
70 |
A2 |
| Student 5 |
9.3 |
14000 |
72 |
A2 |
Consider the weights assumed by the interviewing panel as follows :
CGPA = 30%, Expected Stipend = 20%, Technical Exam Score = 25%, Aptitude Test Grade = 25%
Table 2: The weights of each attribute
| Attribute |
CGPA |
Expected Stipend |
Technical Exam Score |
Aptitude Test Grade |
| Weight |
0.3 |
0.2 |
0.25 |
0.25 |
| Student 1 |
9 |
12000 |
72 |
B1 |
| Student 2 |
7.6 |
8500 |
68 |
B1 |
| Student 3 |
8.2 |
9500 |
63 |
B2 |
| Student 4 |
8.5 |
10000 |
70 |
A2 |
| Student 5 |
9.3 |
14000 |
72 |
A2 |
Two types of attribute:
- A beneficial attribute is one in which a person desires maximum value. Here, CGPA, the technical exam score, and aptitude test scores are beneficial attributes as the company expects the students to have more of these attributes.
- A non-beneficial attribute is one in which minimum values are desired. In this case, the expected stipend is a non-beneficial attribute. The company hikes people who are willing to work more with a low stipend.
Now let’s see which student is to be selected by the company using the Weighted Product Method.
For this, we must normalize the values in Table 2.
- For beneficial attributes,
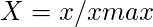
- For non-beneficial attributes,
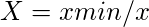
Table 3: Deciding the maximum value for a beneficial attribute and minimum value for non-beneficial attribute
| Attribute |
CGPA |
Expected Stipend |
Technical Exam Score |
Aptitude Test Grade |
| Weight |
0.3 |
0.2 |
0.25 |
0.25 |
| Student 1 |
9 |
12000 |
72(max) |
B1 |
| Student 2 |
7.6 |
8500(min) |
68 |
B1 |
| Student 3 |
8.2 |
9500 |
63 |
B2 |
| Student 4 |
8.5 |
10000 |
70 |
A2(max) |
| Student 5 |
9.3(max) |
14000 |
72 |
A2 |
We will consider the following points for the grade system
A1 – 5
A2 – 4
B1 – 3
B2 – 2
C1 – 1
Table 4: Updating the aptitude test grades
| Attribute |
CGPA |
Expected Stipend |
Technical Exam Score |
Aptitude Test Grade |
| Weight |
0.3 |
0.2 |
0.25 |
0.25 |
| Student 1 |
9 |
12000 |
72(max) |
3 |
| Student 2 |
7.6 |
8500(min) |
68 |
3 |
| Student 3 |
8.2 |
9500 |
63 |
2 |
| Student 4 |
8.5 |
10000 |
70 |
4(max) |
| Student 5 |
9.3(max) |
14000 |
72 |
4 |
Normalize the values for the respective attribute depending on the beneficial and non-beneficial attribute.
Table 5: Normalization
| Attribute |
CGPA |
Expected Stipend |
Technical Exam Score |
Aptitude Test Grade |
| Weight |
0.3 |
0.2 |
0.25 |
0.25 |
| Student 1 |
9/9.3 |
8500/12000 |
72/72 |
3/4 |
| Student 2 |
7.6/9.3 |
8500/8500 |
68/72 |
3/4 |
| Student 3 |
8.2/9.3 |
8500/9500 |
63/72 |
2/4 |
| Student 4 |
8.5/9.3 |
8500/10000 |
70/72 |
4/4 |
| Student 5 |
9.3/9.3 |
8500/14000 |
72/72 |
4/4 |
Table 6: The Weight- Normalized decision matrix
| Attribute |
CGPA |
Expected Stipend |
Technical Exam Score |
Aptitude Test Grade |
| Weight |
0.3 |
0.2 |
0.25 |
0.25 |
| Student 1 |
0.9677 |
0.7083 |
1 |
0.75 |
| Student 2 |
0.8172 |
1 |
0.9444 |
0.75 |
| Student 3 |
0.8817 |
0.8947 |
0.875 |
0.5 |
| Student 4 |
0.9134 |
0.85 |
0.9722 |
1 |
| Student 5 |
1 |
0.6071 |
1 |
1 |
To calculate the weighted product, we take the power of each component with the respective weights as follows
Table 7: Calculation of powers of attributes
| Attribute |
CGPA |
Expected Stipend |
Technical Exam Score |
Aptitude Test Grade |
| Weight |
0.3 |
0.2 |
0.25 |
0.25 |
| Student 1 |
0.96770.3 |
0.70830.2 |
10.25 |
0.750.25 |
| Student 2 |
0.81720.3 |
10.2 |
0.94440.25 |
0.750.25 |
| Student 3 |
0.88170.3 |
0.89470.2 |
0.8750.25 |
0.50.25 |
| Student 4 |
0.91340.3 |
0.850.2 |
0.97220.25 |
10.25 |
| Student 5 |
10.3 |
0.60710.2 |
10.25 |
10.25 |
To calculate the weighted product, we will multiply the value of each attribute in every column row-wise. The value with the highest weighted product is given the higher rank.
Table 8: Calculating the weighted product and finding the rank
| Attribute |
CGPA |
Expected Stipend |
Technical Exam Score |
Aptitude Test Grade |
Performance Score |
Rank |
| Weight |
0.3 |
0.2 |
0.25 |
0.25 |
| Student 1 |
0.96770.3 |
0.70830.2 |
10.25 |
0.750.25 |
0.860064 |
4 |
| Student 2 |
0.81720.3 |
10.2 |
0.94440.25 |
0.750.25 |
0.863481 |
3 |
| Student 3 |
0.88170.3 |
0.89470.2 |
0.8750.25 |
0.50.25 |
0.765907 |
5 |
| Student 4 |
0.91340.3 |
0.850.2 |
0.97220.25 |
10.25 |
0.935451 |
1 |
| Student 5 |
10.3 |
0.60710.2 |
10.25 |
10.25 |
0.905007 |
2 |
You can refer the link below to understand the
Weighted Sum Method here.
Share your thoughts in the comments
Please Login to comment...