Weibull Plot
Last Updated :
16 Aug, 2021
Weibull plot is a graphical technique to determining if the dataset comes from a population that is logically be fit by a 2-parameter Weibull distribution. Before, discussing the Weibull plot in detail, we first need to know about Weibull distribution.
Weibull Distribution:
The formula for probability density distribution for Weibull distribution is:
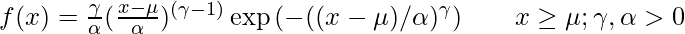
where, Y (gamma) is the shape parameter, u (mu) is called location parameter and ∝ (alpha) is called scale parameter. The case where u=0 and ∝ =1 is called standard weibull distribution.
Two -parameter Weibull distribution:
Two parameters Weibull distribution is the special case of Weibull distribution in which u=0. In this case, the equation for standard Weibull distribution reduces to:
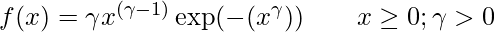
The formula for the cumulative distribution function of Weibull distribution is:
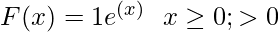
Weibull plot
The Weibull plot have special scales of axes that if the dataset in the weibull distribution, then the points will be in an almost straight line. The least-square fit of the line gives the shape and scale parameter of the Weibull distribution considering the location parameter to be 0.
The Weibull distribution also has the property that a scale parameter passes 63.2% points irrespective of the value of the shape parameter. In this plot, we draw a horizontal line at 63.2% of the y-axis. The x-axis component of the point where it intersects the least square fitted line is called the scale parameter.
Weibull plot is formed of the following two axes:
- Vertical Axis: Weibull cumulative probability in terms of percentage
- Horizontal Axis: Ordered failure times (in Log10 scale).
The vertical scale is derived by formula:
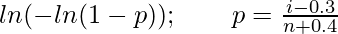
Where, i is the rank of the observation.
Weibull plot is used to answer the following questions:
- Did the distribution follow a 2-parameter Weibull distribution?
- The best estimate for the shape parameter of 2-parameter Weibull distribution?
- The best estimate for the scale parameter of 2-parameter Weibull distribution?
Applications:
The Weibull plot is generally used in the following areas:
- In failure analysis and reliability engineering.
- Warranty analysis
- Estimation of the lifetime of different alloys and implants.
Implementation
- In this implementation, we will also use Weibull library as well as some common data science packages (Numpy, Pandas, and Seaborn). All these libraries are preinstalled in Colab and can be installed in the local environment with pip install.
- For this code, we will be using a VANGEL Tensile Strength dataset. The dataset can be downloaded from here.
Python3
import pandas as pd
import matplotlib.pyplot as plt
import scipy.stats as ss
import numpy as np
import seaborn as sns
import weibull
gamma_1 = np.random.weibull(a=1,size=1000)
gamma_half = np.random.weibull(a=0.5,size=1000)
gamma_5 = np.random.weibull(a=5,size=1000)
gamma_10 = np.random.weibull(a=10,size=1000)
sns.set_style('darkgrid')
fig, ax = plt.subplots(2,2)
sns.histplot(gamma_1,kde=True,ax= ax[0,0] )
ax[0,0].set_title('Gamma = 1 ')
sns.histplot(gamma_half,kde=True, ax= ax[0,1], legend='Y=0.5')
ax[0,1].set_ylim([0,200])
ax[0,1].set_title('Gamma = 0.5 ')
sns.histplot(gamma_5,kde=True, ax= ax[1,0], legend='Y=5')
ax[1,0].set_title('Gamma = 5 ')
sns.histplot(gamma_10,kde=True, ax= ax[1,1], legend='Y=10')
ax[1,1].set_title('Gamma = 10 ')
plt.show()
specimen_strength = pd.read_csv('tensile strength.txt', header=None)
specimen_strength.head()
analysis=weibull.Analysis(specimen_strength[0])
analysis.fit(method='lr')
print(f'shape Parameter: {analysis.beta: .02f}')
print(f'Scale Parameter: {analysis.eta: .02f}')
analysis.stats
analysis.probplot()
|

Standard Weibull Distribution @ different value of shape parameter
0
-----------------
0 25.722681
1 24.319706
2 31.007387
3 25.240414
4 35.406261
shape Parameter: 3.55
Scale Parameter: 31.87
r_squared 0.96102
p_value 7.32837e-71
fit method linear regression
confidence 0.9
beta lower limit 3.1598
beta nominal 3.55485
beta upper limit 3.9993
eta lower limit 30.284
eta nominal 31.8747
eta upper limit 33.5488
mean life 28.7029
median life 28.7521
b10 life 16.9246
dtype: object

Weibull Probability plot
- From the above graph, we can infer that the data is closely following Weibull distribution with the given value of shape and scale parameter.
References:
Share your thoughts in the comments
Please Login to comment...