Ways to write N as sum of two or more positive integers | Set-2
Last Updated :
20 Aug, 2022
Given a number N, the task is to find the number of ways N can be partitioned, i.e. the number of ways that N can be expressed as a sum of positive integers.
Note: N should also be considered itself a way to express it as a sum of positive integers.
Examples:
Input: N = 5
Output: 7
5 can be partitioned in the following ways:
5
4 + 1
3 + 2
3 + 1 + 1
2 + 2 + 1
2 + 1 + 1 + 1
1 + 1 + 1 + 1 + 1
Input: N = 10
Output: 42
This post has been already discussed in Ways to write n as sum of two or more positive integers. In this post, an efficient approach is discussed.
Approach(Using Euler’s recurrence):
If p(n) is the number of partitions of N, then it can be generated by the following generating function:
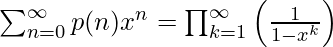
Using this formula and Euler’s pentagonal number theorem, we can derive the following recurrence relation for p(n): (Check the Wikipedia article for more details)
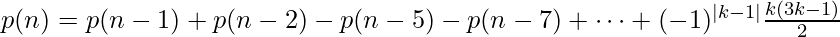
where k = 1, -1, 2, -2, 3, -3, … and p(n) = 0 for n < 0.
Below is the implementation of above approach:
C++
#include <bits/stdc++.h>
using namespace std;
long long partitions(int n)
{
vector<long long> p(n + 1, 0);
p[0] = 1;
for (int i = 1; i <= n; ++i) {
int k = 1;
while ((k * (3 * k - 1)) / 2 <= i) {
p[i] += (k % 2 ? 1 : -1) * p[i - (k * (3 * k - 1)) / 2];
if (k > 0)
k *= -1;
else
k = 1 - k;
}
}
return p[n];
}
int main()
{
int N = 20;
cout << partitions(N);
return 0;
}
|
Java
class GFG
{
static long partitions(int n)
{
long p[] = new long[n + 1];
p[0] = 1;
for (int i = 1; i <= n; ++i)
{
int k = 1;
while ((k * (3 * k - 1)) / 2 <= i)
{
p[i] += (k % 2 != 0 ? 1 : -1) *
p[i - (k * (3 * k - 1)) / 2];
if (k > 0)
{
k *= -1;
}
else
{
k = 1 - k;
}
}
}
return p[n];
}
public static void main(String[] args)
{
int N = 20;
System.out.println(partitions(N));
}
}
|
Python 3
def partitions(n):
p = [0] * (n + 1)
p[0] = 1
for i in range(1, n + 1):
k = 1
while ((k * (3 * k - 1)) / 2 <= i) :
p[i] += ((1 if k % 2 else -1) *
p[i - (k * (3 * k - 1)) // 2])
if (k > 0):
k *= -1
else:
k = 1 - k
return p[n]
if __name__ == "__main__":
N = 20
print(partitions(N))
|
C#
using System;
class GFG
{
static long partitions(int n)
{
long []p = new long[n + 1];
p[0] = 1;
for (int i = 1; i <= n; ++i)
{
int k = 1;
while ((k * (3 * k - 1)) / 2 <= i)
{
p[i] += (k % 2 != 0 ? 1 : -1) *
p[i - (k * (3 * k - 1)) / 2];
if (k > 0)
{
k *= -1;
}
else
{
k = 1 - k;
}
}
}
return p[n];
}
public static void Main(String[] args)
{
int N = 20;
Console.WriteLine(partitions(N));
}
}
|
PHP
<?php
function partitions($n)
{
$p = array_fill(0, $n + 1, 0);
$p[0] = 1;
for ($i = 1; $i < $n + 1; $i++)
{
$k = 1;
while (($k * (3 * $k - 1)) / 2 <= $i)
{
$p[$i] += (($k % 2 ? 1 : -1) *
$p[$i - ($k * (3 * $k - 1)) / 2]);
if ($k > 0)
$k *= -1;
else
$k = 1 - $k;
}
}
return $p[$n];
}
$N = 20;
print(partitions($N));
?>
|
Javascript
<script>
function partitions(n)
{
var p = Array(n + 1).fill(0);
p[0] = 1;
for (i = 1; i <= n; ++i)
{
var k = 1;
while ((k * (3 * k - 1)) / 2 <= i)
{
p[i] += (k % 2 != 0 ? 1 : -1) * p[i - (k * (3 * k - 1)) / 2];
if (k > 0) {
k *= -1;
} else {
k = 1 - k;
}
}
}
return p[n];
}
var N = 20;
document.write(partitions(N));
</script>
|
Time Complexity: O(N?N)
Space Complexity: O(N), since N extra space has been taken.
Share your thoughts in the comments
Please Login to comment...