Ways to form a group from three groups with given constraints
Last Updated :
17 Apr, 2023
Given three numbers(x, y and z) which denote the number of people in the first group, the second group, and third group. We can form groups by selecting people from the first group, the second group and third group such that the following conditions are not void.
- A minimum of one people has to be selected from every group.
- The number of people selected from the first group has to be at least one more than the number of people selected from the third group.
The task is to find the number of ways of forming distinct groups.
Examples:
Input: x = 3, y = 2, z = 1
Output: 9
Lets say x has people (a, b, c)
Y has people (d, e)
Z has people (f)
Then the 9 ways are {a, b, d, f}, {a, b, e, f}, {a, c, d, f}, {a, c, e, f},
{b, c, d, f}, {b, c, e, f}, {a, b, c, d, f}, {a, b, c, e, f} and
{a, b, c, d, e, f}
Input: x = 4, y = 2, z = 1
Output: 27
The problem can be solved using combinatorics. There are three positions(in terms of people from different groups) which need to be filled. The first has to be filled with a number with one or greater than the second position. The third can be filled with any number. We know if we need to fill k positions with N people, then the number of ways of doing it is 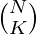 . Hence the following steps can be followed to solve the above problem.
. Hence the following steps can be followed to solve the above problem.
- The second position can be filled with i = 1 to i = y people.
- The first position can be filled with j = i+1 to j = x people.
- The third position can be filled with any number of k = 1 to k = z people.
- Hence the common thing is filling the third position with k people. Hence we can take that portion as common.
- Run two loops( i and j) for filling up the second position and first position respectively.
- The number of ways of filling up the positions is
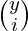 *
* 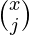 .
. - After calculation of all ways to fill up those two positions, we can simply multiply summation of
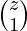 +
+ 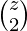 + …
+ … 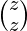 since that was the common part in both.
since that was the common part in both.
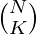 can be pre-computed using Dynamic Programming to reduce time complexity. The method is discussed here.
can be pre-computed using Dynamic Programming to reduce time complexity. The method is discussed here.
Below is the implementation of the above approach.
C++
#include <bits/stdc++.h>
using namespace std;
int C[1000][1000];
void binomialCoeff(int n)
{
int i, j;
for (i = 0; i <= n; i++) {
for (j = 0; j <= i; j++) {
if (j == 0 || j == i)
C[i][j] = 1;
else
C[i][j] = C[i - 1][j - 1] + C[i - 1][j];
}
}
}
int numberOfWays(int x, int y, int z)
{
binomialCoeff(max(x, max(y, z)));
int sum = 0;
for (int i = 1; i <= z; i++) {
sum = (sum + C[z][i]);
}
int sum1 = 0;
for (int i = 1; i <= y; i++) {
for (int j = i + 1; j <= x; j++) {
sum1 = (sum1 + (C[y][i] * C[x][j]));
}
}
sum1 = (sum * sum1);
return sum1;
}
int main()
{
int x = 3;
int y = 2;
int z = 1;
cout << numberOfWays(x, y, z);
return 0;
}
|
Java
class GFG
{
static int C[][] = new int [1000][1000];
static void binomialCoeff(int n)
{
int i, j;
for (i = 0; i <= n; i++)
{
for (j = 0; j <= i; j++)
{
if (j == 0 || j == i)
C[i][j] = 1;
else
C[i][j] = C[i - 1][j - 1] + C[i - 1][j];
}
}
}
static int numberOfWays(int x, int y, int z)
{
binomialCoeff(Math.max(x, Math.max(y, z)));
int sum = 0;
for (int i = 1; i <= z; i++)
{
sum = (sum + C[z][i]);
}
int sum1 = 0;
for (int i = 1; i <= y; i++)
{
for (int j = i + 1; j <= x; j++)
{
sum1 = (sum1 + (C[y][i] * C[x][j]));
}
}
sum1 = (sum * sum1);
return sum1;
}
public static void main(String args[])
{
int x = 3;
int y = 2;
int z = 1;
System.out.println(numberOfWays(x, y, z));
}
}
|
Python3
C = [[0 for i in range(1000)]
for i in range(1000)]
def binomialCoeff(n):
i, j = 0, 0
for i in range(n + 1):
for j in range(i + 1):
if (j == 0 or j == i):
C[i][j] = 1
else:
C[i][j] = C[i - 1][j - 1] + \
C[i - 1][j]
def numberOfWays(x, y, z):
binomialCoeff(max(x, max(y, z)))
sum = 0
for i in range(1, z + 1):
sum = (sum + C[z][i])
sum1 = 0
for i in range(1, y + 1):
for j in range(i + 1, x + 1):
sum1 = (sum1 + (C[y][i] * C[x][j]))
sum1 = (sum * sum1)
return sum1
x = 3
y = 2
z = 1
print(numberOfWays(x, y, z))
|
C#
using System;
class GFG
{
static int [,]C = new int [1000,1000];
static void binomialCoeff(int n)
{
int i, j;
for (i = 0; i <= n; i++)
{
for (j = 0; j <= i; j++)
{
if (j == 0 || j == i)
C[i,j] = 1;
else
C[i,j] = C[i - 1,j - 1] + C[i - 1,j];
}
}
}
static int numberOfWays(int x, int y, int z)
{
binomialCoeff(Math.Max(x, Math.Max(y, z)));
int sum = 0;
for (int i = 1; i <= z; i++)
{
sum = (sum + C[z,i]);
}
int sum1 = 0;
for (int i = 1; i <= y; i++)
{
for (int j = i + 1; j <= x; j++)
{
sum1 = (sum1 + (C[y,i] * C[x,j]));
}
}
sum1 = (sum * sum1);
return sum1;
}
public static void Main(String []args)
{
int x = 3;
int y = 2;
int z = 1;
Console.WriteLine(numberOfWays(x, y, z));
}
}
|
Javascript
<script>
var C = Array(1000).fill().map(()=>Array(1000).fill(0));
function binomialCoeff(n) {
var i, j;
for (i = 0; i <= n; i++) {
for (j = 0; j <= i; j++) {
if (j == 0 || j == i)
C[i][j] = 1;
else
C[i][j] = C[i - 1][j - 1] + C[i - 1][j];
}
}
}
function numberOfWays(x , y , z) {
binomialCoeff(Math.max(x, Math.max(y, z)));
var sum = 0;
for (i = 1; i <= z; i++) {
sum = (sum + C[z][i]);
}
var sum1 = 0;
for (i = 1; i <= y; i++) {
for (j = i + 1; j <= x; j++) {
sum1 = (sum1 + (C[y][i] * C[x][j]));
}
}
sum1 = (sum * sum1);
return sum1;
}
var x = 3;
var y = 2;
var z = 1;
document.write(numberOfWays(x, y, z));
</script>
|
Time Complexity: O(max(x, y, z)^2), due to the computation of binomial coefficients using dynamic programming.
Auxiliary Space: O(max(x, y, z)^2) to store the precomputed binomial coefficients in the 2D array C.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...