Ways of filling matrix such that product of all rows and all columns are equal to unity
Last Updated :
25 Jul, 2022
We are given three values 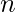 ,
, 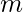 and
and 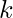 where
where 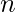 is number of rows in matrix,
is number of rows in matrix, 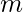 is number of columns in the matrix and
is number of columns in the matrix and 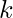 is the number that can have only two values -1 and 1. Our aim is to find the number of ways of filling the matrix of
is the number that can have only two values -1 and 1. Our aim is to find the number of ways of filling the matrix of  such that the product of all the elements in each row and each column is equal to
such that the product of all the elements in each row and each column is equal to 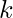 . Since the number of ways can be large we will output
. Since the number of ways can be large we will output 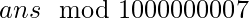
Examples:
Input : n = 2, m = 4, k = -1
Output : 8
Following configurations satisfy the conditions:-


Input : n = 2, m = 1, k = -1
Output : The number of filling the matrix
are 0
From the above conditions, it is clear that the only elements that can be entered in the matrix are 1 and -1. Now we can easily deduce some of the corner cases
- If k = -1, then the sum of number of rows and columns cannot be odd because -1 will be present odd
number of times in each row and column therefore if the sum is odd then answer is 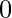 .
. - If n = 1 or m = 1 then there is only one way of filling the matrix therefore answer is 1.
- If none of the above cases are applicable then we fill the first
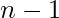 rows and the first
rows and the first 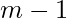 columns with 1 and -1. Then the remaining numbers can be uniquely identified since the product of each row an each column is already known therefore the answer is
columns with 1 and -1. Then the remaining numbers can be uniquely identified since the product of each row an each column is already known therefore the answer is 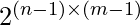 .
.
Implementation:
C++
#include <bits/stdc++.h>
using namespace std;
#define mod 100000007
long long modPower(long long a, long long t)
{
long long now = a, ret = 1;
while (t) {
if (t & 1)
ret = now * (ret % mod);
now = now * (now % mod);
t >>= 1;
}
return ret;
}
long countWays(int n, int m, int k)
{
if (k == -1 && (n + m) % 2 == 1)
return 0;
if (n == 1 || m == 1)
return 1;
return (modPower(modPower((long long)2, n - 1),
m - 1) % mod);
}
int main()
{
int n = 2, m = 7, k = 1;
cout << countWays(n, m, k);
return 0;
}
|
Java
import java.io.*;
class Example {
final static long mod = 100000007;
static long modPower(long a, long t, long mod)
{
long now = a, ret = 1;
while (t > 0) {
if (t % 2 == 1)
ret = now * (ret % mod);
now = now * (now % mod);
t >>= 1;
}
return ret;
}
static long countWays(int n, int m, int k)
{
if (n == 1 || m == 1)
return 1;
else if ((n + m) % 2 == 1 && k == -1)
return 0;
return (modPower(modPower((long)2, n - 1, mod),
m - 1, mod) % mod);
}
public static void main(String args[]) throws IOException
{
int n = 2, m = 7, k = 1;
System.out.println(countWays(n, m, k));
}
}
|
Python3
def modPower(a, t):
now = a;
ret = 1;
mod = 100000007;
while (t):
if (t & 1):
ret = now * (ret % mod);
now = now * (now % mod);
t >>= 1;
return ret;
def countWays(n, m, k):
mod= 100000007;
if (k == -1 and ((n + m) % 2 == 1)):
return 0;
if (n == 1 or m == 1):
return 1;
return (modPower(modPower(2, n - 1),
m - 1) % mod);
n = 2;
m = 7;
k = 1;
print(countWays(n, m, k));
|
C#
using System;
class Example
{
static long mod = 100000007;
static long modPower(long a, long t,
long mod)
{
long now = a, ret = 1;
while (t > 0)
{
if (t % 2 == 1)
ret = now * (ret % mod);
now = now * (now % mod);
t >>= 1;
}
return ret;
}
static long countWays(int n, int m,
int k)
{
if (n == 1 || m == 1)
return 1;
else if ((n + m) % 2 == 1 && k == -1)
return 0;
return (modPower(modPower((long)2, n - 1,
mod), m - 1, mod) % mod);
}
public static void Main()
{
int n = 2, m = 7, k = 1;
Console.WriteLine(countWays(n, m, k));
}
}
|
PHP
<?php
$mod = 100000007;
function modPower($a, $t)
{
global $mod;
$now = $a; $ret = 1;
while ($t)
{
if ($t & 1)
$ret = $now * ($ret % $mod);
$now = $now * ($now % $mod);
$t >>= 1;
}
return $ret;
}
function countWays($n, $m, $k)
{
global $mod;
if ($k == -1 and ($n + $m) % 2 == 1)
return 0;
if ($n == 1 or $m == 1)
return 1;
return (modPower(modPower(2, $n - 1),
$m - 1) % $mod);
}
$n = 2;
$m = 7;
$k = 1;
echo countWays($n, $m, $k);
?>
|
Javascript
<script>
let mod = 100000007;
function modPower(a, t, mod)
{
let now = a, ret = 1;
while (t > 0)
{
if (t % 2 == 1)
ret = now * (ret % mod);
now = now * (now % mod);
t >>= 1;
}
return ret;
}
function countWays(n, m, k)
{
if (n == 1 || m == 1)
return 1;
else if ((n + m) % 2 == 1 && k == -1)
return 0;
return (modPower(modPower(2, n - 1, mod),
m - 1, mod) % mod);
}
let n = 2, m = 7, k = 1;
document.write(countWays(n, m, k));
</script>
|
Output:
64
Time complexity:
*** QuickLaTeX cannot compile formula:
*** Error message:
Error: Nothing to show, formula is empty
.Space Complexity : O(1).
Share your thoughts in the comments
Please Login to comment...