Puzzle 68 | Walking down the hill

I can walk 3 miles per hour uphill and 4 miles per hour on flat land and 6 miles per hour downhill. If I reached the beach nearby me, walking for 50 minutes and I walked back home in 1 hour, can you calculate the total distance from my house to the beach? (Note: I walk with the same uniform speed.)

Solution: This might seem like an incomplete data problem, but it is not.

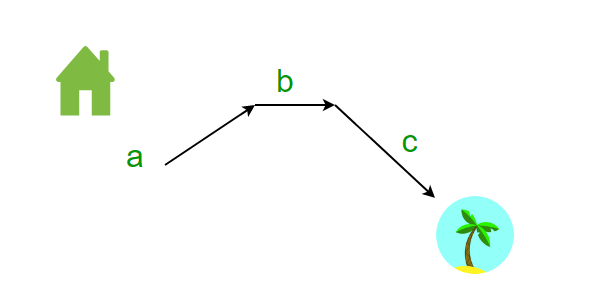
Let us assume that I walk in total from my home to the beach

a mile’s uphill
b miles on flat land
c miles’ downhill
The total distance is a+b+c

When walking from beach to my home, uphill will be downhill and vice versa

Therefore,

c miles’ uphill
b miles on flat land
a mile’s downhill
The total distance is a+b+c

distance/speed = time

By solving the above two, we get two equations

a/3 + b/4 + c/6 = 50/60 hours
c/3 + b/4 + a/6 = 1 hour
=> 2a + 3b + 4c = 12

2c + 3b + 4a = 10

Now we need the distance a + b + c

By adding the above two equations, we get

6a + 6b + 6c = 22

Therefore a + b + c = 22/6 = 11/3 miles or 3 and 2/3 miles

This puzzle is contributed by Harika Mulumudi. Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above

My Personal Notes arrow_drop_up

Save