Wald Test
Last Updated :
18 Jul, 2021
Prerequisite : Maximum Likelihood Estimate
NOTE : It is advised to read the prerequisite article before moving on to Wald Test.
Wald Test : It is a hypothesis test done on the parameters calculated by the Maximum Likelihood Estimate (MLE). It checks if the value of the true input parameters has the same likelihood as the parameters calculated by MLE. In simple words, the larger this wald estimate value, the less likely it is that the input parameters is true. Let us understand in-depth the working of wald test. Observe the formula given below:
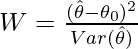
where,
θ_hat -> a vector of all parameters estimated by the maximum likelihood.
θ0 -> a vector of all true input parameters considered under null hypothesis. (H0)
W -> Wald estimate.
Intuition
We consider the initial values of the parameters under the null hypothesis, H0. Now the question remains whether we should accept the null hypothesis and move forward with these parameter values or reject them. This is where the wald test comes into picture.
Wald test tells the difference measure between parameters under the null hypothesis and the ones estimated by the maximum likelihood estimate. If this difference is very large, the wald estimate value is also large. Hence, we reject the null hypothesis and consider the parameters estimated by the MLE.
If this difference measure is small, then the wald estimate value is also small, and we do not reject the null hypothesis. Consider the image given below for in-depth understanding. (Fig 1)

Fig 1 : Intuition
In the above image, we see the Likelihood of the sample y under parameters θ on the y axis. We see that the horizontal difference in θ0 and θ_hat is similar in case of the red and green pdf curves. However, the interpretation of the difference measure both is done differently. See the following two cases given below:
Case 1 : Green probability distribution function
In this case, we see that there is a huge difference in the likelihood value of θ_hat and θ0. So, here the variance of θ_hat is relatively small, hence the wald estimate tends to be quite high. This implies that parameters estimated under null hypothesis H0 are way different than the one calculated by MLE. Hence, we reject the null hypothesis.
Case 2 : Red probability distribution function
However, in this case the value of likelihood of θ_hat and θ0 is quite similar. So, the variance of θ_hat here is quite large, hence making the wald estimate to be quite low. Therefore, we can consider the true values of parameters for the sample data y. Hence, we do not need to reject the null hypothesis.
Wald test can be used to test the associativity between the independent variables dependent variable. A Wald test can be used in a great variety of different models including models for dichotomous variables and models for continuous variables. It has tons of applications in many areas of statistics. Any time a likelihood based approach is used for estimation (e.g., logistic regression, etc) the wald test is used. For any doubt/query, comment below.
Share your thoughts in the comments
Please Login to comment...