Volume of Solid of Revolution: A solid of revolution is a three-dimensional shape created by spinning a two-dimensional curve around a line within the same plane. The volume of such a solid can be computed using integration. The most typical techniques for determining the volume include the disc method, the shell method, and Washer Method.
Volume of Solid of Revolution is generated by revolving a plane area R about a line L known as the axis of revolution in the plane. We use the concept of definite integrals to find the volume of the curve that revolves around any line.
Here in this article, we will learn about the Volume of Solids of Revolution, Disk Method, Washer Method, Examples, and others in detail.
Volume of Solid of Revolution
If we rotate any curve along the line then the figure so formed is a 3-D structure and its volume is found using the concept of integration. Suppose we take a curve y = f(x) that revolves around the x-axis the 3-D shape so formed is shown in the image added below:

If we are given the equation of the curve we can easily find the volume of the shape so formed in a bounded region. The volume of the shape is easily found when the equation of the curve is given in Parametric Form, or Polar Form.
Parametric Form
If the equation of the curve in parametric form i.e.
Where t varies from t1 to t2, then the volume of revolution:
About x-Axis
 [Tex]= \int_{t_{1}}^{t_{2}}\pi g^{2}(t) \frac{df(t)}{dt}dt
[/Tex]
[Tex]= \int_{t_{1}}^{t_{2}}\pi g^{2}(t) \frac{df(t)}{dt}dt
[/Tex]
About y-Axis
 [Tex]= \int_{t_{1}}^{t_{2}}\pi f^{2}(t) \frac{dg(t)}{dt}dt
[/Tex]
[Tex]= \int_{t_{1}}^{t_{2}}\pi f^{2}(t) \frac{dg(t)}{dt}dt
[/Tex]
Polar form
Equation of curve in polar form is, r = f(θ), where θ varies from θ1 to θ2
The volume of revolution is calculated using the formula,
About Initial Line OX i.e., x-Axis (θ = 0)
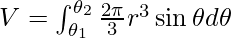
About Line Perpendicular to Initial Line i.e. along OY (θ = π/2)
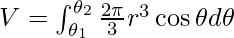
Volume of the revolution is the volume of the curve formed by revolving a solid curve either in the x-axis or in the y-axis. We use integration to find the area of an curve in a fixed interval. For example suppose we want to find the area of the curve y = x3 in the region x = 0 and x = 3 then it is simpily given using the Integration,
Area = 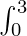 x3dx
x3dx
Now suppose if the same curve is rotated along the x-axis then the voulume of the shape so formed is caculated using the formula,
V = 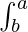 π|f(x)|2 dx
π|f(x)|2 dx
If the curve is rotated along the y-axis then the voulume of the shape so formed is caculated using the formula,
V = 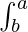 π|f(y)|2 dy
π|f(y)|2 dy
This method of finding the volume of the figure is called the Disck method. We will learn about this method below in the article.
Methods of Volumes of Solids of Revolution
There are two methods to find the volume of the figure that are
Disk Method
Disck Method is the method of finding the volume of the 3-D figure in this method, we take axis of revolution the boundary of the plane region and the cross sections are taken perpendicular to the axis of the revolution. Now the cross section area of the disk is the πr2 and the volume of the disk is the area times its thickness.
- If the disk is perpendicular to the x-axis then its radius is the function of x.
- f the disk is perpendicular to the y-axis then its radius is the function of y.
Now volume of the solid generated by revolving the curve y = f(x) and the axis of the rotion is x-axis then its volume in the interval [a, b] is,
V = 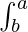 π|f(x)|2 dx
π|f(x)|2 dx
If the volume of the solid generated by revolving the curve x = f(y) and the axis of the rotion is y-axis then its volume in the interval [a, b] is,
V = 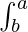 π|f(y)|2 dy
π|f(y)|2 dy
Washer Method
In Washer Method we take the axis of revolution is not the boundary of the plane region and the cross section are taken perpendicular to the axis of revolution. Washer are considered to be the disk with hole. Now to calculate the area of the washer the formula is, π(R2 – r2) and its volume is the area times its thickness.
Now volume of the solid generated by revolving the region bounded by y = f(x) and y = g(x) in the interval [a, b] if f(x) ≥ g(x) then its volume about x-axis is,
V = 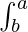 π{|f(x)|2 – |g(x)|2} dx
π{|f(x)|2 – |g(x)|2} dx
If the region is bounded by x = f(y) and x = g(y) in the interval [a, b] if f(y) ≥ g(y) then its volume about y-axis is,
V = 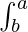 π{|f(y)|2 – |g(y)|2} dy
π{|f(y)|2 – |g(y)|2} dy
People Also Read:
Volume of Solid of Revolution Examples
Example 1: Determine the volume of a solid of revolution generated by revolving the curve whose parametric equations are,
x = 2t + 3 and y = 4t2 – 9. About the x-axis for t = -3/2 to 3/2
Solution:
Volume of a solid revolved about the x-axis when the equation is in parametric form is,
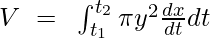
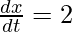
Substituting the given value,

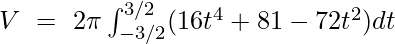
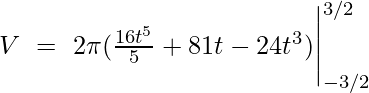
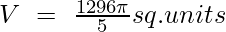
Example 2: Find the volume of solid generated by revolving curve r = 2a cos θ about the initial line OX.
Solution:
Volume of solid generated by revolving about OX when the equation is in polar form is,
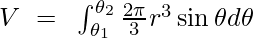
Also for OX, θ = 0 So,

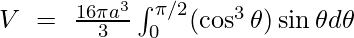
Substituting the given value,
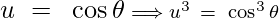
Substituting the given value,
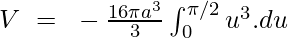
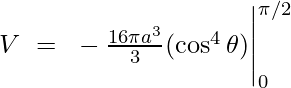
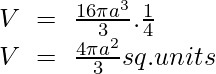
Volume of Solid of Revolution Problems
Q1. Find the volume of the solid generated by revolving the region bounded by y = 4x3 and the x‐axis in the interval [2, 4].
Q2. Find the volume of the solid generated by revolving the region bounded by x = 4y4 and the y‐axis in the interval [-3, 3].
Q3. Find the volume of the solid generated by revolving the region bounded by y = x2 and the y‐axis in the interval [0, 7].
Q4. Find the volume of the solid generated by revolving the region bounded by y = 2x and the x‐axis in the interval [-4, 0].
FAQs on Volume of Solid of Revolution
What is the Formula for the Volume of Revolutions?
The formula used for finding the volume of the revolution of the solid is,
- V =
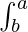 π(f(x))2dx
π(f(x))2dx - V =
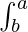 π(f(y))2dy
π(f(y))2dy
What is the Volume of a Revolved Polygon?
Volume of the revolved polygon is found using the Pappus’s Centroid Theorem then the formula for the same is,
V = 2π(A)r
where,
- V is the Volume of 3-D figure
- A is the Area of the Polygon
- r is the Distance between Centroid and Axis of Rotation
What is the Volume of Revolution of a Circle?
Volume of the revolution of the circle is given by the formula, V = πr2·(Thickness)
What is the Surface of Revolution?
Surface of Revolution is defined as the Euclidean space created by rotating any curve one full revolution around any axis of rotation.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...