Volume of largest right circular cylinder within a Sphere
Last Updated :
20 Aug, 2022
Given a sphere of radius 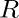 . The task is to find volume of the biggest right circular cylinder that can be inscribed within it.
. The task is to find volume of the biggest right circular cylinder that can be inscribed within it.
Examples:
Input : R = 4
Output : 77.3495
Input : R = 5
Output : 151.073

Approach:
let r be the radius of the right circular cylinder, and h be it’s height.
Volume of the cylinder, V = ?*r2*h
Also, r2 = R2 – h2
or, V = ?*(R2 – h2)*h
or, dV/dh = ?*(R2 – 3*h2)
Setting it to zero, we get h = R/?3
So, Vmax = 2?R3/3?3
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
float cyl(float R)
{
if (R < 0)
return -1;
float V = (2 * 3.14 * pow(R, 3)) / (3 * sqrt(3));
return V;
}
int main()
{
float R = 4;
cout << cyl(R) << endl;
return 0;
}
|
Java
import java.io.*;
class GFG
{
static float cyl(float R)
{
if (R < 0)
return -1;
float V = (float)((2 * 3.14 * Math.pow(R, 3)) /
(3 * Math.sqrt(3)));
return V;
}
public static void main (String[] args)
{
float R = 4;
System.out.print( cyl(R));
}
}
|
Python 3
import math
def cyl(R):
if (R < 0):
return -1
V = ((2 * 3.14 * math.pow(R, 3)) /
(3 * math.sqrt(3)));
return float(V)
R = 4
print(cyl(R))
|
C#
using System;
class GFG
{
static float cyl(float R)
{
if (R < 0)
return -1;
float V = (float)((2 * 3.14 * Math.Pow(R, 3)) /
(3 * Math.Sqrt(3)));
return V;
}
public static void Main ()
{
float R = 4;
Console.WriteLine( cyl(R));
}
}
|
PHP
<?php
function cyl($R)
{
if ($R < 0)
return -1;
$V = (2 * 3.14 * pow($R, 3)) / (3 * sqrt(3));
return $V;
}
$R = 4;
echo cyl($R);
?>
|
Javascript
<script>
function cyl(R)
{
if (R < 0)
return -1;
var V = ((2 * 3.14 * Math.pow(R, 3)) /
(3 * Math.sqrt(3)));
return V;
}
var R = 4;
document.write( cyl(R).toFixed(4));
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...