Visualizing the Bivariate Gaussian Distribution in R
Last Updated :
03 May, 2022
The Gaussian distribution (better known as the normal distribution) is one of the most fundamental probability distributions in statistics. A bivariate Gaussian distribution consists of two independent random variables. One can notice a bell curve while visualizing a bivariate gaussian distribution. Two random variables X1 and X2 are bivariate normal if aX1+bX2 has a normal distribution for all a, b ∈ R.
Probability Distribution Function (PDF) of a bivariate gaussian distribution
The density function describes the relative likelihood of a random variable X at a given sample. Mathematically the PDF of two variables X and Y in bivariate Gaussian distribution is given by:
![Rendered by QuickLaTeX.com P(x_{1},x_{2})=\frac{1}{2\pi \sigma_{1} \sigma_{2} \sqrt{1-\rho^2}} \exp{ \left[ \frac{-z}{2(1-\rho^2)}\right]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-783b8278081815000e0fd0bf15473d14_l3.png)
where,
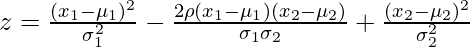
- μ = mean
- σ = standard deviation
- ρ = correlation of x1 and x2
If P = 2 then this is a bivariate gaussian distribution.
Visualizing the Bivariate Gaussian Distribution in R
We will visualize bivariate Gaussian distribution in R by plotting them using the functions from the mnormt() package.
install.packages('mnormt')We will use dmnorm( ) to simulate a normal distribution.
dmnorm( ): mnorm(x, mean = rep(0, d), varcov, log = FALSE)
| Parameter | Description |
|---|
| x | a vector of length d where ‘d=ncol(varcov)’. |
| mean | the expected value of the distribution. |
| varcov | variance-covariance matrix of the distribution. |
| log | if ‘TRUE’ computes the logarithm of the density. |
Now, we will use the contour( ) function to create a contour plot, to get a 2-D visualization of the bivariate gaussian distribution
R
library(mnormt)
set.seed(0)
x1 <- seq(-4, 4, 0.1)
x2 <- seq(-5, 5, 0.1)
mean <- c(0, 0)
cov <- matrix(c(2, -1, -1, 2), nrow=2)
f <- function(x1, x2) dmnorm(cbind(x1, x2), mean, cov)
y <- outer(x1, x2, f)
contour(x1, x2, y)
|
n : sample size.
mean : mean of each variable.
cov : covariance matrix of the two variables.
Output:
For 3-D visualization of the distribution, we will create a surface plot using persp( ) function of the package.
persp(x = seq(0, 1, length.out = nrow(z)),y = seq(0, 1, length.out = ncol(z)),z, xlim = range(x), ylim = range(y),zlim = range(z, na.rm = TRUE),xlab = NULL, ylab = NULL, zlab = NULL,main = NULL, sub = NULL,theta = 0, phi = 15, r = sqrt(3), d = 1,scale = TRUE, expand = 1,col = “white”, border = NULL, theta = -135, lphi = 0,shade = NA, box = TRUE, axes = TRUE, nticks = 5,ticktype = “simple”, …)
| Parameter | Description |
|---|
| x, y | location of grid lines. |
| xlim, ylim, zlim | x-, y- and z-limits. |
| xlab, ylab, zlab | titles for the axes. |
| theta, phi | angles defining the viewing direction. |
| expand | a expansion factor applied to the z coordinates. |
| col | the color(s) of the surface facets. |
| border | the color of the line drawn around the surface facets. |
| shade | the shade at a surface facet. |
| box | should the bounding box for the surface be displayed. |
| ticktype | types of ticks. |
R
install.packages('mnormt')
library(mnormt)
set.seed(0)
x1 <- seq(-4, 4, 0.1)
x2 <- seq(-5, 5, 0.1)
mean <- c(0, 0)
cov <- matrix(c(2, -1, -1, 2), nrow=2)
f <- function(x1, x2) dmnorm(cbind(x1, x2), mean, cov)
y <- outer(x1, x2, f)
persp(x1, x2, y, theta=-20, phi=20, col = 'blue',
expand=0.8, ticktype='detailed')
|
Output:
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...