Vector Projection using Python

A vector is a geometric object which has both magnitude (i.e. length) and direction. A vector is generally represented by a line segment with a certain direction connecting the initial point A and the terminal point B as shown in the figure below and is denoted by

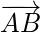
Projection of a Vector on another vector

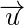
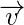
The projection of a vector onto another vector is given as 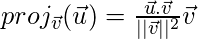Computing vector projection onto another vector in Python:

# import numpy to perform operations on vector
import numpy as np

u = np.array([1, 2, 3])   # vector u
v = np.array([5, 6, 2])   # vector v:

# Task: Project vector u on vector v

# finding norm of the vector v
v_norm = np.sqrt(sum(v**2))

# Apply the formula as mentioned above
# for projecting a vector onto another vector
# find dot product using np.dot()
proj_of_u_on_v = (np.dot(u, v)/v_norm**2)*v

print("Projection of Vector u on Vector v is: ", proj_of_u_on_v)

Output:

Projection of Vector u on Vector v is:  [1.76923077 2.12307692 0.70769231]

One liner code for projecting a vector onto another vector:

(np.dot(u, v)/np.dot(v, v))*v

Projection of a Vector onto a Plane

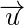
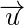
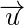
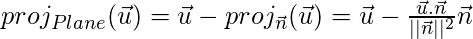
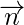
The projection of a vector onto a plane is calculated by subtracting the component of which is orthogonal to the plane from . where, is the plane normal vector. Computing vector projection onto a Plane in Python:

# import numpy to perform operations on vector
import numpy as np

# vector u
u = np.array([2, 5, 8])

# vector n: n is orthogonal vector to Plane P
n = np.array([1, 1, 7])

# Task: Project vector u on Plane P

# finding norm of the vector n
n_norm = np.sqrt(sum(n**2))

# Apply the formula as mentioned above
# for projecting a vector onto the orthogonal vector n
# find dot product using np.dot()
proj_of_u_on_n = (np.dot(u, n)/n_norm**2)*n

# subtract proj_of_u_on_n from u:
# this is the projection of u on Plane P
print("Projection of Vector u on Plane P is: ", u - proj_of_u_on_n)

Output:

Projection of Vector u on Plane P is:  [ 0.76470588  3.76470588 -0.64705882]