Vector Projection Formula
Last Updated :
02 Apr, 2024
Vector Projection is basically the shadow of a vector over another vector. The projection vector is obtained by multiplying the vector with the Cos of the angle between the two vectors. A vector is one which has both magnitude and direction. Two vectors are said to be equal if they have the same magnitude as well as the direction. Vector Projection is essential in solving numerical in physics and mathematics.
In this article, we will learn about what is vector projection, vector projection formula example, the vector projection formula, vector projection formula derivation, vector projection formula linear algebra, vector projection formula 3d and some other related concepts in detail.
What is Vector Projection?
Vector Projection is a method of rotating a vector and placing it on a second vector. Hence, a vector is obtained when a vector is resolved into two components, parallel and perpendicular. The parallel vector is called the Projection Vector. Thus, the Vector Projection is the length of the shadow of a vector over another vector. The vector projection of a vector is obtained by multiplying the vector with the Cos of the angle between the two vectors. Let’s say we have two vectors ‘a’ and ‘b’ and we have to find the projection of the vector a on vector b then we will multiply the vector ‘a’ with cosθ where θ is the angle between vector a and vector b.
If 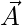 is represented as A and
is represented as A and 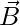 is represented as B, the Vector Projection of A on B is given as the product of A with Cosθ where θ is the angle between A and B. The other formula for Vector Projection of A on B is given as the product of A and B divided by the magnitude of B. The Projection Vector obtained so is a scalar multiple of A and has a direction in the direction of B.
is represented as B, the Vector Projection of A on B is given as the product of A with Cosθ where θ is the angle between A and B. The other formula for Vector Projection of A on B is given as the product of A and B divided by the magnitude of B. The Projection Vector obtained so is a scalar multiple of A and has a direction in the direction of B.
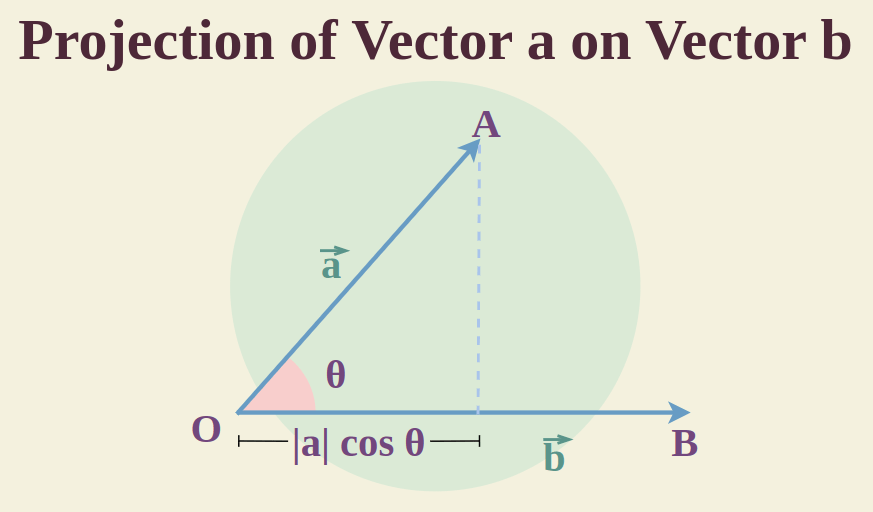
The vector projection formula derivation is discussed below:
Let us assume, OP = 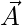 and OQ =
and OQ = 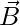 and the angle between OP and OQ is θ. Drawn PN perpendicular to OQ.
and the angle between OP and OQ is θ. Drawn PN perpendicular to OQ.
In the right triangle OPN, Cos θ = ON/OP
⇒ ON = OP Cos θ
⇒ ON = |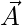 | Cos θ
| Cos θ
ON is the projection vector of 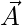 on
on 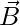
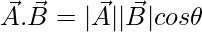
⇒ 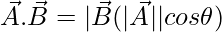
⇒ 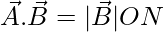
⇒ ON = 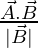
Hence, the ON = 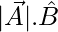
Thus the Vector Projection of 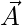 on
on 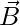 is given as
is given as 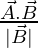
the Vector Projection of 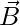 on
on 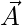 is given as
is given as 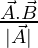
Check: Types of Vectors
Vector Projection Important Terms
To find the vector projection we need to learn to find the angle between two vectors and also to calculate the dot product between two vectors.
Angle Between Two Vectors
The angle between the two vectors is given as the inverse of the cosine of the dot product of two vectors divided by the product of the magnitude of two vectors.
Let’s say we have two vectors 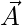 and
and 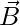 angle between them is θ
angle between them is θ
⇒ cos θ = 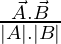
⇒ θ = cos-1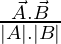
Dot Product of Two Vectors
Let’s say we have two vectors 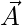 and
and 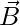 defined as
defined as 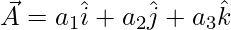 and
and 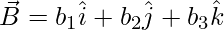 then dot product between them is given as
then dot product between them is given as
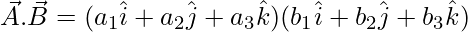
⇒ 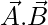 = a1b1 + a2b2 +a3b3
= a1b1 + a2b2 +a3b3
Read More,
Example 1. Find the projection of the vector 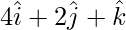 and
and 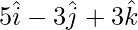 .
.
Solution:
Here,  .
.
We know, projection of Vector a on Vector b = 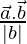
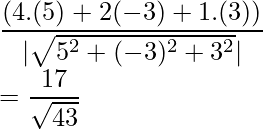
Example 2. Find the projection of the vector  and
and 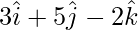
Solution:
Here, 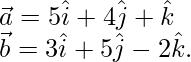
We know, projection of Vector a on Vector b = 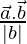
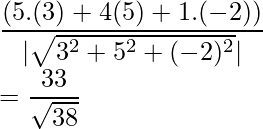
Example 3. Find the projection of the vector 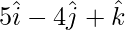 and
and 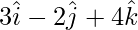
Solution:
Here, 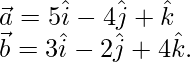
We know, projection of Vector a on Vector b = 
Example 4. Find the projection of the vector  and
and  .
.
Solution:
Here, 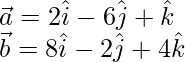
We know, projection of Vector a on Vector b = 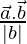
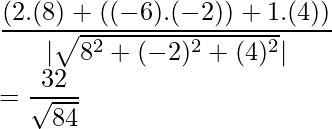
Example 5. Find the projection of the vector 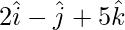 and
and 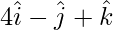 .
.
Solution:
Here, 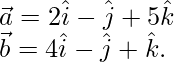
We know, projection of Vector a on Vector b = 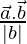
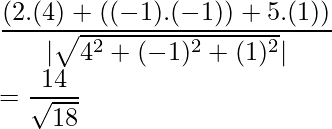
Check: Vector Operations
Practical Applications and Significance
Physics
- Force Decomposition: In physics, the vector projection formula is crucial for decomposing forces into components parallel and perpendicular to surfaces. For example, understanding the force exerted by a rope in a game of tug-of-war requires projecting the force vector onto the direction of the rope.
- Work Calculation: The work done by a force during displacement is calculated using vector projection. The work is the dot product of the force vector and the displacement vector, essentially projecting one vector onto another to find the component of force in the direction of displacement.
Engineering
- Structural Analysis: Engineers use vector projection to analyze stresses on components. By projecting force vectors onto structural axes, they can determine the stress components in different directions, aiding in the design of safer and more efficient structures.
- Fluid Dynamics: In fluid dynamics, vector projection helps in analyzing fluid flow around objects. By projecting velocity vectors of fluid onto surfaces, engineers can study flow patterns and forces, crucial for aerodynamic design and hydraulic engineering.
Computer Graphics
- Rendering Techniques: Vector projection is fundamental in computer graphics for rendering shadows and reflections. By projecting light vectors onto surfaces, graphics software calculates the angles and intensities of shadows and reflections, enhancing realism in 3D models.
- Animation and Game Development: In animation, vector projection is used to simulate movements and interactions. For instance, determining how a character moves over uneven terrain involves projecting motion vectors onto the terrain surface, allowing for realistic animations.
Check: Basis Vectors in Linear Algebra
Real-World Problem-Solving Examples
Example 1: GPS Navigation
- Context: In GPS navigation systems, vector projection is used to calculate the shortest path between two points on the earth’s surface.
- Application: By projecting the displacement vector between two geographical locations onto the earth’s surface vector, GPS algorithms can accurately calculate distances and directions, optimizing travel routes.
Example 2: Sports Analytics
- Context: In sports analytics, particularly in soccer or basketball, vector projection helps in analyzing player movements and ball trajectories.
- Application: By projecting the movement vectors of players onto the game field or court, analysts can study patterns, speeds, and efficiency of movements, contributing to strategic planning and performance improvement.
Example 3: Renewable Energy Engineering
- Context: In the design of wind turbines, understanding the wind force components is essential for optimizing energy production.
- Application: Engineers project wind velocity vectors onto the plane of the turbine blades. This analysis helps in determining the optimal angle and orientation of blades to maximize the capture of wind energy.
Example 4: Augmented Reality (AR)
- Context: In augmented reality applications, vector projection is used to accurately place virtual objects in real-world spaces.
- Application: By projecting vectors from virtual objects onto real-world planes captured by AR devices, developers can ensure that virtual objects interact realistically with the environment, enhancing user experience.
Check: Components of Vector
Vector Projection – FAQs
Define Projection Vector.
The Projection Vector is the shadow of a vector on another vector.
What is the Vector Projection Formula?
The Formula for Projection of Vector is given as 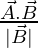
How to Find Projection Vector?
The projection vector is found by calculating the dot product of the two vectors divided by the on which the shadow is cast.
What are Concepts Required to Calculate Projection Vector?
We need to know the angle between two vectors and dot product of two vectors to calculate vector projection.
Where is Projection Vector Used?
Projection Vector is used to solve various physics numerical that require the vector quantity to be split into its components.
What is the Significance of Vector Projection in Physics?
In physics, vector projection is crucial for decomposing forces, calculating work done by a force in a specific direction, and analyzing motion. It helps in understanding how different components of a vector contribute to effects in various directions.
Can Vector Projection be Negative?
Yes, the scalar component of a vector projection can be negative if the angle between the two vectors is greater than 90 degrees, indicating that the projection goes in the opposite direction of the base vector.
How is Vector Projection Used in Engineering?
Engineers use vector projection to analyze structural stresses, optimize designs by decomposing forces into manageable components, and in fluid dynamics to study flow patterns against surfaces.
What’s the Difference Between Scalar and Vector Projection?
Scalar projection gives the magnitude of one vector along the direction of another and can be positive or negative. Vector projection, on the other hand, not only considers the magnitude but also gives the direction of the projection as a vector.
What are Real-World Applications of Vector Projection?
Vector projection has applications in GPS navigation, sports analytics, computer graphics for rendering shadows and reflections, and in augmented reality for placing virtual objects in real-world spaces.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...