Variability in R Programming

Last Updated : 10 May, 2020

Variability (also known as Statistical Dispersion) is another feature of descriptive statistics. Measures of central tendency and variability together comprise of descriptive statistics. Variability shows the spread of a data set around a point.

Example: Suppose, there exist 2 data sets with the same mean value:

A = 4, 4, 5, 6, 6
Mean(A) = 5

B = 1, 1, 5, 9, 9
Mean(B) = 5

So, to differentiate among the two data sets, R offers various measures of variability.

Measures of Variablity

Following are some of the measures of variablity that R offers to differentiate between data sets:

Variance
Standard Deviation
Range
Mean Deviation
Interquartile Range

Variance

Variance is a measure that shows how far is each value from a particular point, preferably mean value. Mathematically, it is defined as the average of squared differences from the mean value.

Formula: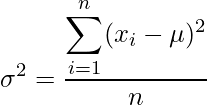

$\displaystyle \sigma^2 = \frac{\displaystyle\sum_{i=1}^{n}(x_i - \mu)^2} {n}$

where,

$\sigma^2$ specifies variance of the data set
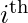$x_i$ specifies $i^{\text{th}}$ value in data set
$\mu$ specifies the mean of data set
n specifies total number of observations

In the R language, there is a standard built-in function to calculate the variance of a data set.

Syntax: var(x)

Parameter:
x: It is data vector

Example:

# Defining vector 
x <- c(5, 5, 8, 12, 15, 16) 
  
# Print variance of x 
print(var(x)) 

Output:

[1] 23.76667

Standard Deviation

Standard deviation in statistics measures the spreaness of data values with respect to mean and mathematically, is calculated as square root of variance.

Formula: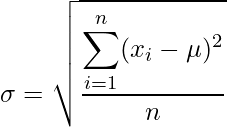
$\displaystyle \sigma = \sqrt{\frac{\displaystyle\sum_{i=1}^{n}(x_i - \mu)^2} {n}}$

where,

$\sigma$ specifies standard deviation of the data set
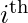$x_i$ specifies $i^{\text{th}}$ value in data set
$\mu$ specifies the mean of data set
n specifies total number of observations

In R language, there is no standard built-in function to calculate the standard deviation of a data set. So, modifying the code to find the standard deviation of data set.

Example:

# Defining vector 
x <- c(5, 5, 8, 12, 15, 16) 
  
# Standard deviation 
d <- sqrt(var(x)) 
  
# Print standard deviation of x 
print(d) 

Output:

[1] 4.875107

Range

Range is the difference between maximum and minimum value of a data set. In R language, max() and min() is used to find the same, unlike range() function that returns the minimum and maximum value of data set.

Example:

# Defining vector 
x <- c(5, 5, 8, 12, 15, 16) 
  
# range() function output 
print(range(x)) 
  
# Using max() and min() function 
# to calculate the range of data set 
print(max(x)-min(x)) 

Output:

[1]  5 16
[1] 11

Mean Deviation

Mean deviation is a measure calculated by taking an average of the arithmetic mean of the absolute difference of each value from the central value. Central value can be mean, median, or mode.

Formula: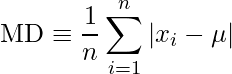
$\displaystyle \mathrm{MD} \equiv \frac{1}{n} \sum_{i=1}^{n}\left|x_{i}-\mu\right|$

where,

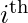$x_i$ specifies $i^{\text{th}}$ value in data set
$\mu$ specifies the mean of data set
n specifies total number of observations

In R language, there is no standard built-in function to calculate mean deviation. So, modifying the code to find mean deviation of the data set.

Example:

# Defining vector 
x <- c(5, 5, 8, 12, 15, 16) 
  
# Mean deviation 
md <- sum(abs(x-mean(x)))/length(x) 
  
# Print mean deviation 
print(md) 

Output:

[1] 4.166667

Interquartile Range

Interquartile Range is based on splitting a data set into parts called as quartiles. There are 3 quartile values (Q1, Q2, Q3) that divide the whole data set into 4 equal parts. Q2 specifies the median of the whole data set.

Mathematically, the interquartile range is depicted as:

IQR = Q3 – Q1

where,

Q3 specifies the median of n largest values
Q1 specifies the median of n smallest values

In R language, there is built-in function to calculate the interquartile range of data set.

Syntax: IQR(x)

Parameter:
x: It specifies the data set

Example:

# Defining vector 
x <- c(5, 5, 8, 12, 15, 16) 
  
# Print Interquartile range 
print(IQR(x)) 

Output:

[1] 8.5

My Personal Notes

Related Articles

Measures of Variablity

Variance

Standard Deviation

Range

Mean Deviation

Interquartile Range