Unique element in an array where all elements occur K times except one | Set 2
Last Updated :
19 Apr, 2023
Given an array arr[] where every element occurs K times except one element which occurs only once, the task is to find that unique element.
Examples:
Input: arr[] = {12, 1, 12, 3, 12, 1, 1, 2, 3, 2, 2, 3, 7}, k = 3
Output: 7
Explanation:
7 is the only element which occurs once while others occurs k times.
Input: arr[] = {12, 12, 2, 2, 3}, k = 2
Output: 3
Explanation:
3 is the only element which occurs once while others occurs k times.
Naive Approach: Suppose we have every element K times then the difference between the sum of all elements in the given array and the K*sum of all unique elements is (K-1) times the unique element.
For Example:
arr[] = {a, a, a, b, b, b, c, c, c, d}, k = 3
unique elements = {a, b, c, d}
Difference = 3*(a + b + c + d) – (a + a + a + b + b + b + c + c + c + d) = 2*d
Therefore, Generalizing the equation:
The unique element can be given by:
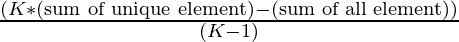
Below are the steps:
- Store all the elements of the given array in the set to get the unique elements.
- Find the sum of all elements in the array (say sum_array) and the sum of all the elements in the set(say sum_set).
- The unique element is given by (K*sum_set – sum_array)/(K – 1).
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int findUniqueElements(int arr[], int N,
int K)
{
unordered_set<int> s(arr, arr + N);
int arr_sum = accumulate(arr, arr + N, 0);
int set_sum = accumulate(s.begin(),
s.end(),
0);
cout << (K * set_sum - arr_sum) / (K - 1);
}
int main()
{
int arr[] = { 12, 1, 12, 3, 12, 1,
1, 2, 3, 2, 2, 3, 7 };
int N = sizeof(arr) / sizeof(arr[0]);
int K = 3;
findUniqueElements(arr, N, K);
return 0;
}
|
Java
import java.util.*;
class GFG{
static void findUniqueElements(int arr[],
int N, int K)
{
Set<Integer> s = new HashSet<>();
for(int i = 0; i < N; i++)
s.add(arr[i]);
int arr_sum = 0;
for(int i = 0; i < N; i++)
arr_sum += arr[i];
int set_sum = 0;
Iterator it = s.iterator();
while (it.hasNext())
{
set_sum += (int)it.next();
}
System.out.println((K * set_sum - arr_sum) /
(K - 1));
}
public static void main(String[] args)
{
int arr[] = { 12, 1, 12, 3, 12, 1,
1, 2, 3, 2, 2, 3, 7 };
int N = arr.length;
int K = 3;
findUniqueElements(arr, N, K);
}
}
|
Python3
def findUniqueElements(arr, N, K):
s = set()
for x in arr:
s.add(x)
arr_sum = sum(arr)
set_sum = 0
for x in s:
set_sum += x
print((K * set_sum - arr_sum) // (K - 1))
if __name__ == '__main__':
arr = [ 12, 1, 12, 3, 12, 1,
1, 2, 3, 2, 2, 3, 7 ]
N = len(arr)
K = 3
findUniqueElements(arr, N, K)
|
C#
using System;
using System.Collections.Generic;
class GFG{
static void findUniqueElements(int []arr,
int N, int K)
{
HashSet<int> s = new HashSet<int>();
for(int i = 0; i < N; i++)
s.Add(arr[i]);
int arr_sum = 0;
for(int i = 0; i < N; i++)
arr_sum += arr[i];
int set_sum = 0;
foreach(int i in s)
set_sum += i;
Console.WriteLine((K * set_sum - arr_sum) /
(K - 1));
}
public static void Main(String[] args)
{
int []arr = { 12, 1, 12, 3, 12, 1,
1, 2, 3, 2, 2, 3, 7 };
int N = arr.Length;
int K = 3;
findUniqueElements(arr, N, K);
}
}
|
Javascript
<script>
function findUniqueElements(arr, N, K)
{
var s = new Set(arr);
var arr_sum = arr.reduce((a, b) => a + b, 0);
var set_sum = 0;
s.forEach(function(value) {
set_sum += value;
})
document.write(Math.floor((K * set_sum - arr_sum) / (K - 1)));
}
var arr = [ 12, 1, 12, 3, 12, 1,
1, 2, 3, 2, 2, 3, 7 ];
var N = arr.length;
var K = 3;
findUniqueElements(arr, N,K);
</script>
|
Time Complexity: O(N), where N is the number of elements in the array
Auxiliary Space Complexity: O(N/K), where K is the frequency.
Another Approach: The idea is to use hashing but it will take O(n) time and requires extra space. We can also do it by sorting but it will take O(N log N) time.
Efficient Approach: The above problem can be optimized in terms of constant space complexity. Use bit manipulation approach for this problem.
- Let’s assume we have a case where all the elements appear k times except 1 element.
- So, count the bit of every element for 32 bits.
- Count 0th bit of every element and take modulo by k will eliminate the bit of elements which present k times and we remain with the only bit of element which presents one time.
- Apply this process for all the 32 bits and by taking modulo by k we will eliminate repeated elements bits.
- At every step, generate the results from these remaining bits.
- To handle any negative number, check if the result is present in the array or not if present then print it. Else print negative of the result.
For Example arr[] = {2, 2, 4, 2, 2, 2, 1, 1, 1, 1, 1} , k = 5
| Index | Elements | 2nd bit | 1st bit | 0th bit |
| 0 | 2= 010 | 0 | 1 | 0 |
| 1 | 2= 010 | 0 | 1 | 0 |
| 2 | 4 =100 | 1 | 0 | 0 |
| 3 | 2= 010 | 0 | 1 | 0 |
| 4 | 2= 010 | 0 | 1 | 0 |
| 5 | 2= 010 | 0 | 1 | 0 |
| 6 | 1 = 001 | 0 | 0 | 1 |
| 7 | 1 = 001 | 0 | 0 | 1 |
| 8 | 1 = 001 | 0 | 0 | 1 |
| 9 | 1 = 001 | 0 | 0 | 1 |
| 10 | 1 = 001 | 0 | 0 | 1 |
| Sum%k | | 1%5=1 | 5%5=0 | 5%5=0 |
| Result | | 1 | 0 | 0 |
Our result is (100) in binary = 4 in decimal. So the final answer will be 4, because it presents 1 time.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int findunique(vector<int>& a, int k)
{
int res = 0;
for (int i = 0; i < 32; i++) {
int p = 0;
for (int j = 0; j < a.size(); j++) {
p += (abs(a[j]) & (
1 << i)) != 0 ? 1 : 0;
}
p %= k;
res += pow(2, i) * p;
}
int c = 0;
for (auto x : a)
if (x == res) {
c = 1;
break;
}
return c == 1 ? res : -res;
}
int main()
{
vector<int> a = { 12, 12, 2, 2, 3 };
int k = 2;
cout << findunique(a, k) << "\n";
}
|
Java
import java.util.Arrays;
class Main{
public static int findunique(int a[],
int k)
{
int res = 0;
for (int i = 0; i < 32; i++)
{
int p = 0;
for (int j = 0; j < a.length; j++)
{
p += (Math.abs(a[j]) &
(1 << i)) != 0 ? 1 : 0;
}
p %= k;
res += Math.pow(2, i) * p;
}
int c = 0;
for (int x = 0; x < a.length; x++)
if (a[x] == res)
{
c = 1;
break;
}
return c == 1 ? res : -res;
}
public static void main(String[] args)
{
int a[] = {12, 12, 2, 2, 3};
int k = 2;
System.out.println(findunique(a, k));
}
}
|
Python3
def findunique(a, k):
res = 0
for i in range(32):
p = 0
for j in range(len(a)):
if (abs(a[j]) & (1 << i)) != 0 :
p += 1
p %= k
res += pow(2, i) * p
c = 0
for x in a:
if (x == res) :
c = 1
break
if c == 1 :
return res
else :
return -res
a = [ 12, 12, 2, 2, 3 ]
k = 2
print(findunique(a, k))
|
C#
using System;
class GFG{
public static int findunique(int []a,
int k)
{
int res = 0;
for (int i = 0; i < 32; i++)
{
int p = 0;
for (int j = 0; j < a.Length; j++)
{
p += (Math.Abs(a[j]) &
(1 << i)) != 0 ? 1 : 0;
}
p %= k;
res += (int)Math.Pow(2, i) * p;
}
int c = 0;
for (int x = 0; x < a.Length; x++)
if (a[x] == res)
{
c = 1;
break;
}
return c == 1 ? res : -res;
}
public static void Main(string []args)
{
int []a = {12, 12, 2, 2, 3};
int k = 2;
Console.Write(findunique(a, k));
}
}
|
Javascript
<script>
function findunique(a, k)
{
var res = 0;
for (var i = 0; i < 32; i++) {
var p = 0;
for (var j = 0; j < a.length; j++) {
p += (Math.abs(a[j]) & (
1 << i)) != 0 ? 1 : 0;
}
p %= k;
res += Math.pow(2, i) * p;
}
var c = 0;
for (var i =0;i<a.length;i++)
if (a[i] == res) {
c = 1;
break;
}
return c == 1 ? res : -res;
}
var a = [ 12, 12, 2, 2, 3 ];
var k = 2;
document.write( findunique(a, k) + "<br>");
</script>
|
Time Complexity: O(32 * n) = O(n)
Auxiliary Space: O(1)
Using Counter and List Comprehension in python:
Approach:
We can use Python’s Counter module to count the occurrences of each element in the given array. Then, we can filter out the elements that occur k times using list comprehension and find the unique element using set difference operation.
Import the Counter class from the collections module. This will allow us to count the occurrences of each element in the input array.
Define the find_unique_element function that takes an input array arr and an integer k.
Use the Counter class to count the number of occurrences of each element in the input array.
Create a set k_elements that contains all elements in the input array that occur exactly k times.
Create a set unique_elements that contains all elements in the input array that occur less than k times.
Compute the set difference between unique_elements and k_elements to obtain a set containing only the unique element in the input array that occurs less than k times.
Convert the resulting set to a list and return the first element (which is the only element in the set, since it is unique).
Python3
from collections import Counter
def find_unique_element(arr, k):
count = Counter(arr)
k_elements = set([key for key in count if count[key] == k])
unique_element = list(set(arr) - k_elements)[0]
return unique_element
arr1 = [12, 1, 12, 3, 12, 1, 1, 2, 3, 2, 2, 3, 7]
k1 = 3
print(find_unique_element(arr1, k1))
arr2 = [12, 12, 2, 2, 3]
k2 = 2
print(find_unique_element(arr2, k2))
|
Time Complexity: O(n)
Space Complexity: O(n)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...