Types of Quadrilaterals and Their Properties

Types of Quadrilaterals: All the different types of quadrilaterals have very distinct shapes and properties which help us identify these quadrilaterals. As we know, quadrilaterals are polygons with four sides, four interior angles, and four vertices. With its unique sets of properties and characteristics, there can be various quadrilaterals such as square, rectangle, parallelogram, rhombus, trapezium, and kite. 

Understanding these different types of quadrilaterals helps us understand the fundamentals of geometry and also helps us deal with further advanced topics in mathematics such as trigonometry and calculus.

In this article, we will explore the different types of quadrilaterals, their properties, and how they differ from one another. So, let’s dive into the world of different types of quadrilaterals.

What are the types of Quadrilaterals?

The word “Quadrilateral” is a combination of two Latin words ‘Quadri‘ means a variant of four, and ‘latus‘ means side, which has a combined meaning of “four sides”. As we already discussed in the introduction of the article Quadrilaterals can be defined as, types of polygons that have four sides, four vertices, and four angles along with a pair of diagonals.  Other than that, the Sum of the interior angles of quadrilaterals is 360°.

The primary types of quadrilaterals include squares, rectangles, rhombuses, parallelograms, trapezoids (or trapezia), and kites. Squares are highly symmetric with all sides equal and all angles right angles. Rectangles also have right angles but only require opposite sides to be equal. Rhombuses boast equal-length sides with opposite equal angles, similar to a square but generally lacking right angles. Parallelograms have opposite sides that are parallel and equal, with opposite angles equal, forming a more general category that includes squares, rectangles, and rhombuses. Trapezoids have at least one pair of parallel sides, differing in their non-parallel sides and angles. Finally, kites feature two pairs of adjacent sides that are equal, typically with one pair of diagonally opposite angles being equal

Examples of Quadrilaterals

Types of Quadrilaterals

Types of Quadrilaterals

As there are many types of quadrilaterals, with each type having unique sets of properties and characteristics. The most common types of quadrilaterals which we will study in this article are:

• Square
• Rectangle
• Rhombus
• Parallelogram
• Trapezium
• Kite

1. Square

A quadrilateral that has all sides equal and opposite sides parallel and all interior angles equal to 90° is called a Square. The diagram of the square is represented in the following illustration:

Properties of a Square

Some properties of Square are as follows:

• All the sides of a square are equal to each other.
• All the angles of a square are equal and of 90° each.
• Opposite Sides are parallel to each other. 
• Diagonals are perpendicular bisectors of each other and are equal.
• The perimeter of a square is equal to the sum of the lengths of all its sides i.e., 4a (where a is the side of the square).
• The area of a square is equal to the length of one side squared i.e., a² (where a is the side of the square).

Note: All squares are rhombuses but not all rhombuses are squares.

2. Rectangle

A rectangle is a quadrilateral in which there are two pair of equal and parallel sides with all the interior angle right angle, i.e. 90°. The following illustration shows the diagram of a general rectangle.

Properties of a Rectangle

Properties of a rectangle are similar to those of a parallelogram:

• Opposite Sides are parallel to each other.
• Opposite Sides of a rectangle are equal.
• Diagonals bisect each other.
• Diagonals of the rectangle are equal.
• Each interior angle of a rectangle is equal i.e., 90°
• The perimeter of a rectangle is equal to the sum of the lengths of all its sides i.e., 2(l + b) (where l and b are the length and breadth of rectangle respectively).
• The area of a rectangle is equal to the product of its length and width i.e., l × b (where l and b are the length and breadth of the rectangle respectively).

Note: All rectangles are parallelogram, but all parallelograms are not rectangle.

3. Rhombus

A quadrilateral that has all sides equal and opposite sides parallel is called Rhombus. The following illustration shows the general diagram of Rhombus:

Properties of a Rhombus

Properties of a rhombus are similar to those of a parallelogram:

• All the sides of a rhombus are equal to each other.
• Opposite Sides are parallel to each other.
• Opposite angles of a rhombus are equal.
• The diagonals of a rhombus bisect each other.
• The diagonals of a rhombus are perpendicular bisectors of each other.
• The area of a rhombus can be calculated using the formula A = 1/2(d₁×d₂), (where d₁ and d₂ are the lengths of the diagonals.)

Note: Rhombus is a parallelogram with all side equal, but parallelogram is not rhombus.

4. Parallelogram

A parallelogram is a special type of quadrilateral whose opposite sides are equal and parallel.

Properties of Parallelogram

There are different properties of parallelograms.

1. Opposite sides of the Parallelogram are parallel and equal in length.
2. Opposite angles of the Parallelogram are also equal.
3. Any two consecutive or adjacent angle in a parallelogram is supplementary i.e., the sum of any two adjacent angles are 180°.
4. Diagonals of Parallelogram bisect each other.
5. A diagonal of a parallelogram divides it into two congruent triangles.

5. Trapezium

A trapezium is a quadrilateral that has one pair of opposite sides parallel. The following illustration shows the general diagram of a trapezium:

Properties of Trapezium

The different properties of the trapezium are as follows:

• The parallel sides of a trapezium are called bases, and the non-parallel sides are called legs.
• The angles on the same side of the leg are called adjacent angles, and they add up to 180 degrees.
• The diagonals of a trapezium intersect each other.
• The length of the diagonal can be calculated using the formula [Tex]d = \sqrt{(a-b)^2 + h^2}[/Tex], (where a and b are the lengths of the bases and h is the distance between the bases.)
• The area of a trapezium can be calculated using the formula A = 1/2(a+b)h, (where a and b are the lengths of the bases and h is the distance between the bases.)

6. Kite

A kite is a quadrilateral that has two pairs of adjacent sides that are equal in length. The following illustration shows the general diagram of a kite:

Properties of Kite

The different properties of the quadrilateral kite are as follows:

• Kite has two pairs of adjacent sides which are equal in length. 
• The diagonals of a kite are perpendicular to each other.
• Diagonals of kite bisect each other.
• The longer diagonal of a kite bisects the angle between the unequal sides, while the shorter diagonal bisects the angle between the equal sides.
• The area of a kite can be calculated using the formula A = 1/2(d₁×d₂), (where d₁ and d₂ are the lengths of the diagonals).

Table Showing Types of Quadrilateral and their Properties

Quadrilateral Type	Sides	Angles	Diagonals	Symmetry
Square	All four sides equal	All angles are 90°	Diagonals are equal and bisect each other at 90°	Four lines of symmetry; rotational symmetry of 90°
Rectangle	Opposite sides equal	All angles are 90°	Diagonals are equal but do not bisect each other at 90°	Two lines of symmetry; rotational symmetry of 180°
Rhombus	All four sides equal	Opposite angles equal	Diagonals bisect each other at 90° and are not equal	Two lines of symmetry; no rotational symmetry at 90° (only 180°)
Parallelogram	Opposite sides equal	Opposite angles equal	Diagonals bisect each other but are not equal	No line symmetry; rotational symmetry of 180°
Trapezoid	One pair of parallel sides	Only the angles adjacent to each non-parallel side are supplementary	Diagonals are generally not equal and do not bisect each other at 90°	Some have one line of symmetry if isosceles; no rotational symmetry
Kite	Two pairs of adjacent sides equal	One pair of opposite angles equal (the ones between the unequal sides)	One diagonal bisects the other; diagonals are perpendicular	One line of symmetry through the diagonal; no rotational symmetry

Concave and Convex Quadrilaterals

Based on the value of internal angles, quadrilaterals or any other polygon can be classified into concave and convex. 

Concave Quadrilaterals

Those quadrilaterals which have at least one of the interior angles greater than 180° are called concave quadrilaterals. We can also define concave quadrilaterals as those quadrilaterals for which any one of its diagonals lies outside the area bounded by the sides of the quadrilateral. 

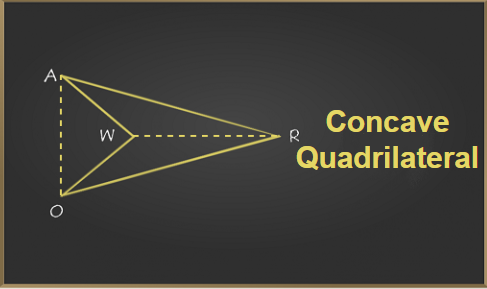
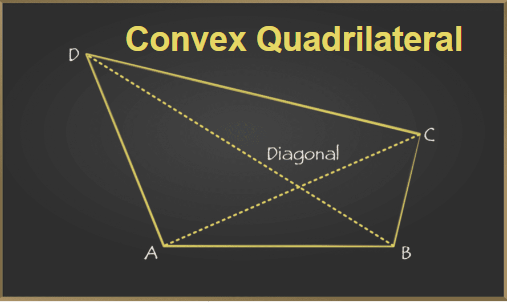
Convex Quadrilaterals

Those quadrilaterals in which all the interior angles are less than 180° are called convex quadrilaterals. We can also define convex quadrilaterals as those quadrilaterals for which none of its diagonals lies outside the area bounded by the sides of the quadrilateral. 

Types of Quadrilaterals Examples

Problem 1: All rhombus are squares or all squares are rhombus. Which of these statements is correct and why?

Solution:

Square and rhombus both have all sides equal, but a rhombus is called square if each of its angle is 90⁰. So all squares can be called rhombus, but converse is not true.

Problem 2: In the figure ROPE is a square. Show that diagonals are equal.

Solution:

In Δ REP and Δ OEP

RE = OP (sides of square

∠E = ∠P (each 90°)

EP = EP (common)

Therefore, triangles are congruent by SAS criteria.

Therefore, RP = OE (c.p.c.t)

Therefore, diagonals of square are equal.

Problem 3: In rectangle ABCD, AO = 5cm. Find the length of diagonal BD. Also, find the perimeter of the rectangle if AB = 8cm and AD = 6cm.

Solution: 

AO = OC = 5cm (diagonals bisect each other)

Therefore, AC = 10cm

BD = AC =10cm (diagonals of rectangle are equal) 

Perimeter = AB + BC + CD + DA

                 = 8 + 6 +8 +6 (opposite sides are equal)

                 = 28cm

Problem 4: In rectangle ABCD, ∠ABD = 3x – 7 and ∠CBA = 6x – 2. Find the value of x.

Solution:

Each angle of rectangle is 90°

Therefore,

 ∠ABD + ∠CBA = 90^°

3x – 7 + 6x – 2 = 90

9x – 9 = 90

9x = 99

x = 11

Problem 5: In rectangle ABCD AO = 2x – 10 cm, OB = x + 4 cm. Find the length of diagonal BD

Solution:

In rectangle diagonals bisect each other and are equal.

Therefore, AO = OB

2x – 10 = x + 4

x = 14

OB = 14 + 4 = 18 cm

OD = 18 cm (as diagonals bisect each other)

Therefore, BD = 36 cm

Problem 6: Diagonals of the rhombus are 24cm and 10cm. Find the side of the rhombus.

Solution:

AC = 24cm

BD = 10cm

Therefore, AO = 12cm and OB = 5cm (diagonals bisect each other)

In right-angled triangle AOB, (diagonals of rhombus are perpendicular)

AB² = OA² + OB²

AB² = 12² + 5²

AB² = 144 + 25

AB² = 169

AB = 13cm

Therefore, side of rhombus is 13cm.

Problem 7: In a rhombus one of the diagonals is equal to a side of the rhombus. Find the angles of the Rhombus.

Solution:

In rhombus PQRS PR = PQ (given)

Therefore, PQ = QR = RS = SP = PR (as all side of rhombus are equal)

In triangle PQR

PQ = QR = PR 

Therefore, it is an equilateral triangle.

∠QPR = ∠Q = ∠QRP = 60^°

>||ly ∠SPR = ∠S = ∠PRS = 60^°

Therefore, angles of rhombus are ∠P = 120^°, ∠Q = 60^°, ∠R = 120^°, ∠S = 60^°

Problem 8: Derive the formula for the area of the rhombus i.e., 1/2 × Product of Diagonals.

Solution:

As diagonals of rhombus bisect each other at right angle.

In rhombus ABCD 

Area of Triangle ABD = 1/2 × BD ×AO (As area of triangle = 1/2 × base× height) . . . (1)

Area of Triangle BCD = 1/2 × BD × CO . . . (2)

Thus, Area of rhombus = Area of triangle ABD + area of triangle BCD

⇒ Area of rhombus = 1/2 × BD × AO + 1/2 × BD × CO

⇒ Area of rhombus = 1/2 × BD (AO + CO)

⇒ Area of rhombus = 1/2 × BD × AC           (AE + CE = AC)

Therefore, area of rhombus = 1/2 × Product of Diagonals

Types of Quadrilaterals Worksheet

1. Identify the type of quadrilateral formed by the following coordinates: A(1, 1), B(4, 2), C(3, 5), D(0, 4).

2. Given a quadrilateral with side lengths of 6 cm, 8 cm, 10 cm, and 12 cm, determine if it is a parallelogram.

3. If one pair of opposite angles in a quadrilateral measures 90 degrees and the other pair measures 120 degrees, what type of quadrilateral is it?

4. In a rhombus, if one diagonal measures 10 cm, what is the length of the other diagonal?

5. A quadrilateral has four congruent sides and four right angles. What type of quadrilateral is it?

FAQs on Types of Quadrilaterals 

Define Quadrilateral.

A quadrilateral is a polygon with four sides and four vertices.

What are the Different Types of Quadrilaterals?

The different types of quadrilaterals are:

• Square
• Rectangle
• Rhombus
• Parallelogram
• Trapezium
• Kite

What is a Rectangle?

A rectangle is a quadrilateral with four right angles and opposite sides of equal length.

What is a Square?

A square is a quadrilateral with four right angles and four sides of equal length.

What is a Parallelogram?

A parallelogram is a quadrilateral with opposite sides parallel and equal in length.

What is a Rhombus?

A rhombus is a quadrilateral with four sides of equal length.

What is a Trapezoid?

A trapezoid is a quadrilateral with one pair of opposite sides parallel.

What is a Kite?

A kite is a quadrilateral with two pairs of adjacent sides that are equal in length, and the diagonals intersect at right angles.

Can a Rectangle also be a Square?

Yes, a rectangle can also be a square if all four sides are of equal length.

Can a Square also be a Rectangle?

Yes, a square can also be a rectangle if all four angles are right angles.

Can a Rhombus also be a Square?

Yes, a rhombus can also be a square if all four angles are right angles.

Can a Square also be a Rhombus?

Yes, a square can also be a rhombus if all four sides are of equal length.

How many Diagonals does a Quadrilateral have?

A quadrilateral has two diagonals.