Two Clique Problem (Check if Graph can be divided in two Cliques)
Last Updated :
16 Mar, 2023
A Clique is a subgraph of graph such that all vertices in subgraph are completely connected with each other. Given a Graph, find if it can be divided into two Cliques.
Examples:
Input : G[][] = {{0, 1, 1, 0, 0},
{1, 0, 1, 1, 0},
{1, 1, 0, 0, 0},
{0, 1, 0, 0, 1},
{0, 0, 0, 1, 0}};
Output : Yes
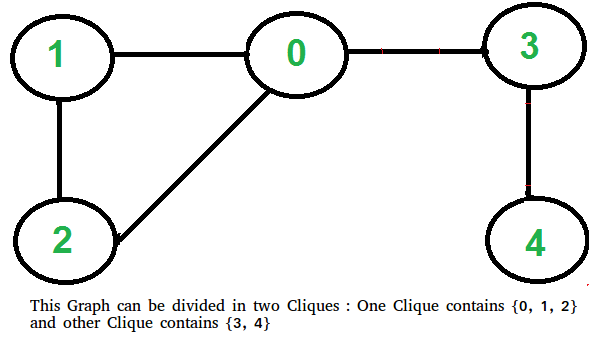
This problem looks tricky at first, but has a simple and interesting solution. A graph can be divided in two cliques if its complement graph is Bipartitite. So below are two steps to find if graph can be divided in two Cliques or not.
- Find the complement of Graph. Below is the complement graph is above shown graph. In complement, all original edges are removed. And the vertices which did not have an edge between them, now have an edge connecting them.
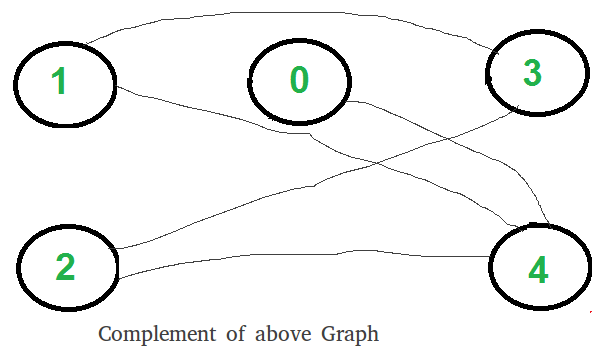
- Return true if complement is Bipartite, else false. The above shown graph is Bipartite. Checking whether a Graph is Bipartite or no is discussed here.
How does this work?
If complement is Bipartite, then graph can be divided into two sets U and V such that there is no edge connecting to vertices of same set. This means in original graph, these sets U and V are completely connected. Hence original graph could be divided in two Cliques.
Implementation:
Below is the implementation of above steps.
C++
#include <bits/stdc++.h>
using namespace std;
const int V = 5;
bool isBipartiteUtil(int G[][V], int src, int colorArr[])
{
colorArr[src] = 1;
queue <int> q;
q.push(src);
while (!q.empty())
{
int u = q.front();
q.pop();
for (int v = 0; v < V; ++v)
{
if (G[u][v] && colorArr[v] == -1)
{
colorArr[v] = 1 - colorArr[u];
q.push(v);
}
else if (G[u][v] && colorArr[v] == colorArr[u])
return false;
}
}
return true;
}
bool isBipartite(int G[][V])
{
int colorArr[V];
for (int i = 0; i < V; ++i)
colorArr[i] = -1;
for (int i = 0; i < V; i++)
if (colorArr[i] == -1)
if (isBipartiteUtil(G, i, colorArr) == false)
return false;
return true;
}
bool canBeDividedinTwoCliques(int G[][V])
{
int GC[V][V];
for (int i=0; i<V; i++)
for (int j=0; j<V; j++)
GC[i][j] = (i != j)? !G[i][j] : 0;
return isBipartite(GC);
}
int main()
{
int G[][V] = {{0, 1, 1, 1, 0},
{1, 0, 1, 0, 0},
{1, 1, 0, 0, 0},
{0, 1, 0, 0, 1},
{0, 0, 0, 1, 0}
};
canBeDividedinTwoCliques(G) ? cout << "Yes" :
cout << "No";
return 0;
}
|
Java
import java.util.ArrayDeque;
import java.util.Deque;
class GFG {
static int V = 5;
static boolean isBipartiteUtil(int G[][], int src, int colorArr[])
{
colorArr[src] = 1;
Deque <Integer> q = new ArrayDeque<>();
q.push(src);
while (!q.isEmpty())
{
int u = q.peek();
q.pop();
for (int v = 0; v < V; ++v)
{
if (G[u][v] == -1 && colorArr[v] == -1)
{
colorArr[v] = 1 - colorArr[u];
q.push(v);
}
else if (G[u][v] == colorArr[u] && colorArr[v] == colorArr[u])
return false;
}
}
return true;
}
static boolean isBipartite(int G[][])
{
int colorArr[]=new int[V];
for (int i = 0; i < V; ++i)
colorArr[i] = -1;
for (int i = 0; i < V; i++)
if (colorArr[i] == -1)
if (isBipartiteUtil(G, i, colorArr) == false)
return false;
return true;
}
static boolean canBeDividedinTwoCliques(int G[][])
{
int GC[][]=new int[V][V];
for (int i=0; i<V; i++)
for (int j=0; j<V; j++)
GC[i][j] = (i != j)? -GC[i][j] : 0;
return isBipartite(GC);
}
public static void main(String[] args) {
int G[][] = {{0, 1, 1, 1, 0},
{1, 0, 1, 0, 0},
{1, 1, 0, 0, 0},
{0, 1, 0, 0, 1},
{0, 0, 0, 1, 0}
};
if(canBeDividedinTwoCliques(G))
System.out.println("Yes");
else
System.out.println("No");
}
}
|
Python3
from queue import Queue
def isBipartiteUtil(G, src, colorArr):
global V
colorArr[src] = 1
q = Queue()
q.put(src)
while (not q.empty()):
u = q.get()
for v in range(V):
if (G[u][v] and colorArr[v] == -1):
colorArr[v] = 1 - colorArr[u]
q.put(v)
elif (G[u][v] and colorArr[v] == colorArr[u]):
return False
return True
def isBipartite(G):
global V
colorArr = [-1] * V
for i in range(V):
if (colorArr[i] == -1):
if (isBipartiteUtil(G, i, colorArr) == False):
return False
return True
def canBeDividedinTwoCliques(G):
global V
GC = [[None] * V for i in range(V)]
for i in range(V):
for j in range(V):
GC[i][j] = not G[i][j] if i != j else 0
return isBipartite(GC)
V = 5
G = [[0, 1, 1, 1, 0],
[1, 0, 1, 0, 0],
[1, 1, 0, 0, 0],
[0, 1, 0, 0, 1],
[0, 0, 0, 1, 0]]
if canBeDividedinTwoCliques(G):
print("Yes")
else:
print("No")
|
Javascript
<script>
const V = 5;
function isBipartiteUtil(G,src,colorArr)
{
colorArr[src] = 1;
let q = [];
q.push(src);
while (q.length > 0)
{
let u = q.shift();
for (let v = 0; v < V; ++v)
{
if (G[u][v] && colorArr[v] == -1)
{
colorArr[v] = 1 - colorArr[u];
q.push(v);
}
else if (G[u][v] && colorArr[v] == colorArr[u])
return false;
}
}
return true;
}
function isBipartite(G)
{
let colorArr = new Array(V);
for (let i = 0; i < V; ++i)
colorArr[i] = -1;
for (let i = 0; i < V; i++)
if (colorArr[i] == -1)
if (isBipartiteUtil(G, i, colorArr) == false)
return false;
return true;
}
function canBeDividedinTwoCliques(G)
{
let GC = new Array(V).fill(0).map(()=>new Array(V));
for (let i=0; i<V; i++)
for (let j=0; j<V; j++)
GC[i][j] = (i != j)? !G[i][j] : 0;
return isBipartite(GC);
}
let G =[[0, 1, 1, 1, 0],
[1, 0, 1, 0, 0],
[1, 1, 0, 0, 0],
[0, 1, 0, 0, 1],
[0, 0, 0, 1, 0]
];
canBeDividedinTwoCliques(G) ? document.write("Yes"):
document.write("No");
</script>
|
C#
using System;
using System.Collections.Generic;
class GFG {
static int V = 5;
static bool IsBipartiteUtil(int[, ] G, int src,
int[] colorArr)
{
colorArr[src] = 1;
Queue<int> q = new Queue<int>();
q.Enqueue(src);
while (q.Count > 0) {
int u = q.Dequeue();
for (int v = 0; v < V; ++v) {
if (G[u, v] == -1 && colorArr[v] == -1) {
colorArr[v] = 1 - colorArr[u];
q.Enqueue(v);
}
else if (G[u, v] == colorArr[u]
&& colorArr[v] == colorArr[u])
return false;
}
}
return true;
}
static bool IsBipartite(int[, ] G)
{
int[] colorArr = new int[V];
for (int i = 0; i < V; ++i)
colorArr[i] = -1;
for (int i = 0; i < V; i++)
if (colorArr[i] == -1)
if (!IsBipartiteUtil(G, i, colorArr))
return false;
return true;
}
static bool CanBeDividedInTwoCliques(int[, ] G)
{
int[, ] GC = new int[V, V];
for (int i = 0; i < V; i++)
for (int j = 0; j < V; j++)
GC[i, j] = (i != j) ? -GC[i, j] : 0;
return IsBipartite(GC);
}
static void Main(string[] args)
{
int[, ] G = { { 0, 1, 1, 1, 0 },
{ 1, 0, 1, 0, 0 },
{ 1, 1, 0, 0, 0 },
{ 0, 1, 0, 0, 1 },
{ 0, 0, 0, 1, 0 } };
if (CanBeDividedInTwoCliques(G))
Console.WriteLine("Yes");
else
Console.WriteLine("No");
}
}
|
Output :
Yes
Time complexity : O(V2)
Space complexity : O(V^2),
Reference:
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...