Tukey-Kramer Test for Post Hoc Analysis
Last Updated :
16 Sep, 2021
If in ANOVA test we come to a conclusion that we have to reject our null hypothesis(H0) and then we know that some treatment or factor level means are different and we wish to find them then we proceed to do post hoc analysis with Tukey’s test to find which pair is different. This method is a multiple comparison method.
About:
- Used to tell about population means having a significant difference.
- Done when H0 is rejected by ANOVA method.
- We need to do pair-wise comparisons in this method.
- Uses critical range to compare absolute mean differences.
Critical Range Formula:
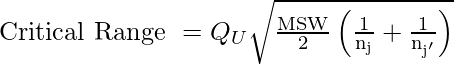
Steps:
- Compute absolute mean differences for all possible pairs.
- Find the Qu value from the standard table.
- Compute the critical range from the formula mentioned above.
- Compare with the results obtained in step 1.
Example:
A fruit company wanted to know the perfect amount of fruit pulp for their juice for that they conducted a survey and asked consumers to rate it on a scale of 0 to 25 on taste. Note taste does not depend on the amount of fruit pulp it depends on artificial pulp.
Following were the results inferred:
| Pulp (%) | Observations | Total | Average |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 5 | 7 | 8 | 15 | 11 | 9 | 10 | 60 | 10.00 |
| 10 | 12 | 17 | 13 | 18 | 19 | 15 | 94 | 15.67 |
| 15 | 14 | 18 | 19 | 17 | 16 | 18 | 102 | 17.00 |
| 20 | 19 | 25 | 22 | 23 | 18 | 20 | 127 | 21.17 |
| | | | | | | | 383 | 15.96 |
Step 1: Computing absolute mean differences:

Step 2:
Here, C = 4 and N-C = 24 – 4 = 20
Let α = 0.05
From the standard Q table Qu = 3.96
Step 3: Put the value obtained above we get Critical Range = 4.124
Step 4: Compare it with every result in Step 1 we get all of the absolute mean differences are greater than the critical range. Other than (X2, X3). Hence we see a significant difference between each pair of means, except 10% concentration and 15% concentration at the 5% level of significance.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...