True Error vs Sample Error
Last Updated :
21 Sep, 2021
True Error
The true error can be said as the probability that the hypothesis will misclassify a single randomly drawn sample from the population. Here the population represents all the data in the world.
Let’s consider a hypothesis h(x) and the true/target function is f(x) of population P. The probability that h will misclassify an instance drawn at random i.e. true error is:
![Rendered by QuickLaTeX.com T.E. = Prob[f(x) \neq h(x)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e24cf50a51b132e08bc521ccd35caffb_l3.png)
Sample Error
The sample error of S with respect to target function f and data sample S is the proportion of examples S misclassifies.
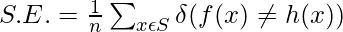
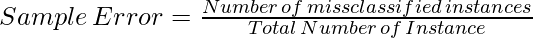
or, the following formula represents also represents sample error:
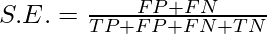
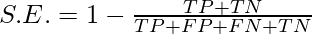
- S.E. = 1- Accuracy
Suppose Hypothesis h misclassifies the 7 out of the 33 examples in total populations. Then the sampling error should be:
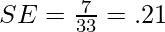
Bias & Variance
Bias: Bias is the difference between the average prediction of the hypothesis and the correct value of prediction. The hypothesis with high bias tries to oversimplify the training (not working on a complex model). It tends to have high training errors and high test errors.
![Rendered by QuickLaTeX.com Bias = E[h(x)]- f(x)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-53fd26a9d8203b3b844122149f90d4b5_l3.png)
Variance: High variance hypotheses have high variability between their predictions. They try to over-complex the model and do not generalize the data very well.
![Rendered by QuickLaTeX.com Var(X) = E[(X - E[X])^2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-98c0a9bb98440d9ce6a930e18a9970eb_l3.png)
Confidence Interval
Generally, the true error is complex and difficult to calculate. It can be estimated with the help of a confidence interval. The confidence interval can be estimated as the function of the sampling error.
Below are the steps for the confidence interval:
- Randomly drawn n samples S (independently of each other), where n should be >30 from the population P.
- Calculate the Sample Error of sample S.
Here we assume that the sampling error is the unbiased estimator of True Error. Following is the formula for calculating true error:
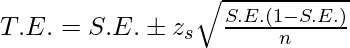
where zs is the value of the z-score of the s percentage of the confidence interval:
| % Confidence Interval | 50 | 80 | 90 | 95 | 99 | 99.5 |
|---|
| Z-score | 0.67 | 1.28 | 1.64 | 1.96 | 2.58 | 2.80 |
|---|
True Error vs Sample Error
| True Error | Sample Error |
|---|
| The true error represents the probability that a random sample from the population is misclassified. | Sample Error represents the fraction of the sample which is misclassified. |
| True error is used to estimate the error of the population. | Sample Error is used to estimate the errors of the sample. |
| True error is difficult to calculate. It is estimated by the confidence interval range on the basis of Sample error. | Sample Error is easy to calculate. You just have to calculate the fraction of the sample that is misclassified. |
| The true error can be caused by poor data collection methods, selection bias, or non-response bias. | Sampling error can be of type population-specific error (wrong people to survey), selection error, sample-frame error (wrong frame window selected for sample), and non-response error (when respondent failed to respond). |
Implementation:
In this implementation, we will be implementing the estimation of true error using a confidence interval.
Python3
import numpy as np
import scipy.stats as st
np.random.seed(0)
data = np.random.randint(10, 30, 10000)
alphas = [0.90, 0.95, 0.99, 0.995]
for alpha in alphas:
print(st.norm.interval(alpha=alpha, loc=np.mean(data), scale=st.sem(data)))
|
# confidence Interval
90%: (17.868667310403545, 19.891332689596453)
95%: (17.67492277275104, 20.08507722724896)
99%: (17.29626006422982, 20.463739935770178)
99.5%: (17.154104780989755, 20.60589521901025)
References:
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...