Trinomial Triangle

The trinomial triangle is a variation of Pascal’s triangle. The difference between the two is that an entry in the trinomial triangle is the sum of the three (rather than the two in Pascal’s triangle) entries above it : 

The k-th entry of the n-th row is denoted by : 

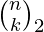
Rows are counted starting from 0. The entries of the n-th row are indexed starting with -n from the left, and the middle entry has index 0. The symmetry of the entries of a row about the middle entry is expressed by the relationship 

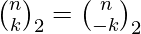
Properties :

• The n-th row corresponds to the coefficients in the polynomial expansion of the expansion of the trinomial (1 + x + x²) raised to the n-th power. 
  
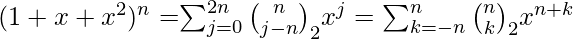
  or Symmetrically
  
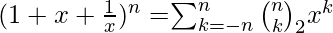
  hence the alternative name trinomial coefficients because of their relationship to the multinomial coefficients : 
  
  
• The diagonals have intersecting properties, such as their relationship to the triangular numbers. 
  
• The sum of the elements of n-th row is 3ⁿ.

Recursion formula
The trinomial coefficients can be generated using the following recursion formula : 


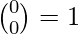
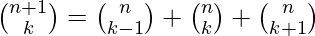
where, 
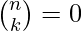, for k n
Applications :

• The triangle corresponds to the number of possible paths that can be taken by the king in a game of chess. The entry in a cell represents the number of different paths (using minimum number of moves) the king can take to reach the cell. 
  

• The coefficient of x^k in the polynomial (1 + x + x²)ⁿ specifies the number of different ways of randomly drawing k cards from two sets of n identical playing cards. For example, in such a card game with two sets of the three cards A, B, C , the choices look like this : 
  

• Given a positive number n. The task is to print Trinomial Triangle of height n. 
  Examples:
  

Input : n = 4
Output :
1
1 1 1
1 2 3 2 1
1 3 6 7 6 3 1

Input : n = 5
Output :
1
1 1 1 
1 2 3 2 1
1 3 6 7 6 3 1
1 4 10 16 19 16 10 4 1

• Below is the implementation of printing trinomial triangle of height n : 
  

C++

// CPP Program to print trinomial triangle.
#include<bits/stdc++.h>
using namespace std;

// Function to find the trinomial triangle value.
int TrinomialValue(int n, int k)
{
    // base case
    if (n == 0 && k == 0)
        return 1;

    // base case
    if(k < -n || k > n)
        return 0;

    // recursive step.
    return TrinomialValue (n - 1, k - 1)
           + TrinomialValue (n - 1, k)
           + TrinomialValue (n - 1, k + 1);
}

// Function to print Trinomial Triangle of height n.
void printTrinomial(int n)
{
    // printing n rows.
    for (int i = 0; i < n; i++)
    {
        // printing first half of triangle
        for (int j = -i; j <= 0; j++)
            cout << TrinomialValue(i, j) << " ";

        // printing second half of triangle.
        for (int j = 1; j <= i; j++)
            cout << TrinomialValue(i, j) << " ";

        cout << endl;
    }
}

// Driven Program
int main()
{
    int n = 4;

    printTrinomial(n);
    return 0;
}

Java

// Java Program to print trinomial triangle.
import java.util.*;
import java.lang.*;

public class GfG {

    // Function to find the trinomial
    // triangle value.
    public static int TrinomialValue(int n,
                                     int k)
    {
        // base case
        if (n == 0 && k == 0)
            return 1;

        // base case
        if (k < -n || k > n)
            return 0;

        // recursive step.
        return TrinomialValue(n - 1, k - 1)
            + TrinomialValue(n - 1, k)
            + TrinomialValue(n - 1, k + 1);
    }

    // Function to print Trinomial
    // Triangle of height n.
    public static void printTrinomial(int n)
    {
        // printing n rows.
        for (int i = 0; i < n; i++)
        {
            // printing first half of triangle
            for (int j = -i; j <= 0; j++)
                System.out.print(TrinomialValue(i, j)
                                    + " ");

            // printing second half of triangle.
            for (int j = 1; j <= i; j++)
                System.out.print(TrinomialValue(i, j)
                                  + " ");

            System.out.println();
        }
    }

    // driver function
    public static void main(String argc[])
    {
        int n = 4;

        printTrinomial(n);
    }

}

/* This code is contributed by Sagar Shukla */

Python3

# Python3 code to print trinomial triangle.

# Function to find the trinomial triangle value.
def TrinomialValue(n, k):
    # base case
    if n == 0 and k == 0:
        return 1

    # base case
    if k < -n or k > n:
        return 0

    # recursive step.
    return (TrinomialValue (n - 1, k - 1)+
                TrinomialValue (n - 1, k)+
                        TrinomialValue (n - 1, k + 1))

# Function to print Trinomial Triangle of height n.
def printTrinomial( n ):

    # printing n rows.
    for i in range(n):

        # printing first half of triangle
        for j in range(-i, 1):
            print(TrinomialValue(i, j),end=" ")

        # printing second half of triangle.
        for j in range(1, i+1):
            print( TrinomialValue(i, j),end=" ")

        print("\n",end='')

# Driven Code
n = 4
printTrinomial(n)

# This code is contributed by "Sharad_Bhardwaj".

C#

// C# Program to print trinomial triangle.
using System;

public class GfG {

    // Function to find the trinomial
    // triangle value.
    public static int TrinomialValue(int n,
                                    int k)
    {
        // base case
        if (n == 0 && k == 0)
            return 1;

        // base case
        if (k < -n || k > n)
            return 0;

        // recursive step.
        return TrinomialValue(n - 1, k - 1)
            + TrinomialValue(n - 1, k)
            + TrinomialValue(n - 1, k + 1);
    }

    // Function to print Trinomial
    // Triangle of height n.
    public static void printTrinomial(int n)
    {
        // printing n rows.
        for (int i = 0; i < n; i++)
        {
            // printing first half of triangle
            for (int j = -i; j <= 0; j++)
                Console.Write(TrinomialValue(i, j)
                                    + " ");

            // printing second half of triangle.
            for (int j = 1; j <= i; j++)
                Console.Write(TrinomialValue(i, j)
                                + " ");

            Console.WriteLine();
        }
    }

    // Driver function
    public static void Main()
    {
        int n = 4;

        printTrinomial(n);
    }

}

/* This code is contributed by Vt_m */

PHP

<?php
// PHP Program to print
// trinomial triangle.

// Function to find the
// trinomial triangle value.
function TrinomialValue($n, $k)
{
    // base case
    if ($n == 0 && $k == 0)
        return 1;

    // base case
    if($k < -$n || $k > $n)
        return 0;

    // recursive step.
    return TrinomialValue ($n - 1, $k - 1) +
           TrinomialValue ($n - 1, $k) +
           TrinomialValue ($n - 1, $k + 1);
}

// Function to print Trinomial
// Triangle of height n.
function printTrinomial($n)
{
    // printing n rows.
    for ($i = 0; $i < $n; $i++)
    {
        // printing first
        // half of triangle
        for ($j = -$i; $j <= 0; $j++)
            echo TrinomialValue($i, $j), " ";

        // printing second
        // half of triangle.
        for ($j = 1; $j <= $i; $j++)
            echo TrinomialValue($i, $j) , " ";

        echo "\n";
    }
}

// Driver Code
$n = 4;

printTrinomial($n);

// This code is contributed
// by ajit
?>

Javascript

<script>

// JavaScript Program to print trinomial triangle.

    // Function to find the trinomial
    // triangle value.
    function TrinomialValue(n, k)
    {
        // base case
        if (n == 0 && k == 0)
            return 1;

        // base case
        if (k < -n || k > n)
            return 0;

        // recursive step.
        return TrinomialValue(n - 1, k - 1)
            + TrinomialValue(n - 1, k)
            + TrinomialValue(n - 1, k + 1);
    }

    // Function to print Trinomial
    // Triangle of height n.
    function printTrinomial(n)
    {
        // printing n rows.
        for (let i = 0; i < n; i++)
        {
            // printing first half of triangle
            for (let j = -i; j <= 0; j++)
                document.write(TrinomialValue(i, j)
                                    + " ");

            // printing second half of triangle.
            for (let j = 1; j <= i; j++)
                document.write(TrinomialValue(i, j)
                                  + " ");

            document.write("<br/>");
        }
    }

// Driver code
        let n = 4;
        printTrinomial(n);

        // This code is contributed by code_hunt.
</script>

Output:

1 
1 1 1 
1 2 3 2 1 
1 3 6 7 6 3 1 

• Below is the implementation of printing Trinomial Triangle using Dynamic Programming and property of trinomial triangle i.e 
  

C++

// C++ Program to print trinomial triangle.
#include <bits/stdc++.h>
#define MAX 10
using namespace std;

// Function to find the trinomial triangle value.
int TrinomialValue(int dp[MAX][MAX], int n, int k)
{
    // Using property of trinomial triangle.
    if (k < 0)
        k = -k;

    // If value already calculated, return that.
    if (dp[n][k] != 0)
        return dp[n][k];

    // base case
    if (n == 0 && k == 0)
        return 1;

    // base case
    if (k < -n || k > n)
        return 0;

    // recursive step and storing the value.
    return (dp[n][k] = TrinomialValue(dp, n - 1, k - 1)
                       + TrinomialValue(dp, n - 1, k)
                       + TrinomialValue(dp, n - 1, k + 1));
}

// Function to print Trinomial Triangle of height n.
void printTrinomial(int n)
{
    int dp[MAX][MAX] = { 0 };

    // printing n rows.
    for (int i = 0; i < n; i++) {
        // printing first half of triangle
        for (int j = -i; j <= 0; j++)
            cout << TrinomialValue(dp, i, j) << " ";

        // printing second half of triangle.
        for (int j = 1; j <= i; j++)
            cout << TrinomialValue(dp, i, j) << " ";

        cout << endl;
    }
}

// Driven Program
int main()
{
    int n = 4;
    printTrinomial(n);
    return 0;
}

// The code is contributed by Gautam goel (gautamgoel962)

C

// CPP Program to print trinomial triangle.
#include<bits/stdc++.h>
#define MAX 10
using namespace std;

// Function to find the trinomial triangle value.
int TrinomialValue(int dp[MAX][MAX], int n, int k)
{
    // Using property of trinomial triangle.
    if (k < 0)
        k = -k;

    // If value already calculated, return that.
    if (dp[n][k] != 0)
        return dp[n][k];

    // base case
    if (n == 0 && k == 0)
        return 1;

    // base case
    if(k < -n || k > n)
        return 0;

    // recursive step and storing the value.
    return (dp[n][k] = TrinomialValue(dp, n - 1, k - 1)
           + TrinomialValue(dp, n - 1, k)
           + TrinomialValue(dp, n - 1, k + 1));
}

// Function to print Trinomial Triangle of height n.
void printTrinomial(int n)
{
    int dp[MAX][MAX] = { 0 };

    // printing n rows.
    for (int i = 0; i < n; i++)
    {
        // printing first half of triangle
        for (int j = -i; j <= 0; j++)
            cout << TrinomialValue(dp, i, j) << " ";

        // printing second half of triangle.
        for (int j = 1; j <= i; j++)
            cout << TrinomialValue(dp, i, j) << " ";

        cout << endl;
    }
}

// Driven Program
int main()
{
    int n = 4;

    printTrinomial(n);
    return 0;
}

Java

// Java Program to print trinomial triangle.
import java.util.*;
import java.lang.*;

public class GfG {

    private static final int MAX = 10;

    // Function to find the trinomial triangle value.
    public static int TrinomialValue(int dp[][], int n, int k)
    {
        // Using property of trinomial triangle.
        if (k < 0)
            k = -k;

        // If value already calculated, return that.
        if (dp[n][k] != 0)
            return dp[n][k];

        // base case
        if (n == 0 && k == 0)
            return 1;

        // base case
        if (k < -n || k > n)
            return 0;

        // recursive step and storing the value.
        return (dp[n][k] = TrinomialValue(dp, n - 1, k - 1)
                           + TrinomialValue(dp, n - 1, k)
                           + TrinomialValue(dp, n - 1, k + 1));
    }

    // Function to print Trinomial Triangle of height n.
    public static void printTrinomial(int n)
    {
        int[][] dp = new int[MAX][MAX];

        // printing n rows.
        for (int i = 0; i < n; i++) {
            // printing first half of triangle
            for (int j = -i; j <= 0; j++)
                System.out.print(TrinomialValue(dp, i, j) + " ");

            // printing second half of triangle.
            for (int j = 1; j <= i; j++)
                System.out.print(TrinomialValue(dp, i, j) + " ");

            System.out.println();
        }
    }

    // driver function
    public static void main(String argc[])
    {
        int n = 4;
        printTrinomial(n);
    }

}
/* This code is contributed by Sagar Shukla */

Python3

# Python3 code to print trinomial triangle.

# Function to find the trinomial triangle value.
def TrinomialValue(dp , n , k):

    # Using property of trinomial triangle.
    if k < 0:
        k = -k

    # If value already calculated, return that.
    if dp[n][k] != 0:
        return dp[n][k]

    # base case
    if n == 0 and k == 0:
        return 1

    # base case
    if k < -n or k > n:
        return 0

    # recursive step and storing the value.
    return  (TrinomialValue(dp, n - 1, k - 1) +
                TrinomialValue(dp, n - 1, k)+
                    TrinomialValue(dp, n - 1, k + 1))

# Function to print Trinomial Triangle of height n.
def printTrinomial(n):
    dp = [[0]*10]*10

    # printing n rows.
    for i in range(n):

        # printing first half of triangle
        for j in range(-i,1):
            print(TrinomialValue(dp, i, j),end=" ")

        # printing second half of triangle.
        for j in range(1,i+1):
            print(TrinomialValue(dp, i, j),end=" ")
        print("\n",end='')

# Driven Program
n = 4
printTrinomial(n)

# This code is contributed by "Sharad_Bhardwaj".

C#

// C# Program to print
// trinomial triangle.
using System;

class GFG
{

    private static int MAX = 10;

    // Function to find the
    // trinomial triangle value.
    public static int TrinomialValue(int [,]dp,
                                     int n, int k)
    {
        // Using property of
        // trinomial triangle.
        if (k < 0)
            k = -k;

        // If value already
        // calculated, return that.
        if (dp[n, k] != 0)
            return dp[n, k];

        // base case
        if (n == 0 && k == 0)
            return 1;

        // base case
        if (k < -n || k > n)
            return 0;

        // recursive step and storing the value.
        return (dp[n, k] = TrinomialValue(dp, n - 1,
                                              k - 1) +
                           TrinomialValue(dp, n - 1,
                                                  k) +
                           TrinomialValue(dp, n - 1,
                                              k + 1));
    }

    // Function to print Trinomial
    // Triangle of height n.
    public static void printTrinomial(int n)
    {
        int[,] dp = new int[MAX, MAX];

        // printing n rows.
        for (int i = 0; i < n; i++)
        {
            // printing first
            // half of triangle
            for (int j = -i; j <= 0; j++)
            Console.Write(TrinomialValue(dp, i,
                                         j) + " ");

            // printing second half
            // of triangle.
            for (int j = 1; j <= i; j++)
                Console.Write(TrinomialValue(dp, i,
                                             j) + " ");

            Console.WriteLine();
        }
    }

    // Driver Code
    static public void Main ()
    {
        int n = 4;
        printTrinomial(n);
    }
}

// This code is contributed by ajit

PHP

<?php
// PHP Program to print
// trinomial triangle.

$MAX = 10;

// Function to find the
// trinomial triangle value.
function TrinomialValue($dp, $n, $k)
{
    // Using property of
    // trinomial triangle.
    if ($k < 0)
        $k = -$k;

    // If value already
    // calculated, return that.
    if ($dp[$n][$k] != 0)
        return $dp[$n][$k];

    // base case
    if ($n == 0 && $k == 0)
        return 1;

    // base case
    if($k < -$n || $k > $n)
        return 0;

    // recursive step and
    // storing the value.
    return ($dp[$n][$k] = TrinomialValue($dp, $n - 1, $k - 1) +
                          TrinomialValue($dp, $n - 1, $k) +
                          TrinomialValue($dp, $n - 1, $k + 1));
}

// Function to print Trinomial
// Triangle of height n.
function printTrinomial($n)
{
    global $MAX;
    $dp;
    for ($i = 0; $i < $MAX; $i++)
    for ($j = 0; $j < $MAX; $j++)
        $dp[$i][$j] = 0;

    // printing n rows.
    for ($i = 0; $i < $n; $i++)
    {
        // printing first
        // half of triangle
        for ($j = -$i; $j <= 0; $j++)
            echo TrinomialValue($dp, $i, $j)." ";

        // printing second
        // half of triangle.
        for ($j = 1; $j <= $i; $j++)
            echo TrinomialValue($dp, $i, $j)." ";

        echo "\n";
    }
}

// Driven Code
$n = 4;
printTrinomial($n);

// This code is contributed by mits
?>

Javascript

<script>


// Javascript Program to print trinomial triangle.
var MAX = 10

// Function to find the trinomial triangle value.
function TrinomialValue(dp, n, k)
{
    // Using property of trinomial triangle.
    if (k < 0)
        k = -k;

    // If value already calculated, return that.
    if (dp[n][k] != 0)
        return dp[n][k];

    // base case
    if (n == 0 && k == 0)
        return 1;

    // base case
    if(k < -n || k > n)
        return 0;

    // recursive step and storing the value.
    return (dp[n][k] = TrinomialValue(dp, n - 1, k - 1)
           + TrinomialValue(dp, n - 1, k)
           + TrinomialValue(dp, n - 1, k + 1));
}

// Function to print Trinomial Triangle of height n.
function printTrinomial(n)
{
    var dp = Array.from(Array(MAX), ()=> Array(MAX).fill(0));

    // printing n rows.
    for (var i = 0; i < n; i++)
    {
        // printing first half of triangle
        for (var j = -i; j <= 0; j++)
            document.write( TrinomialValue(dp, i, j) + " ");

        // printing second half of triangle.
        for (var j = 1; j <= i; j++)
            document.write( TrinomialValue(dp, i, j) + " ");

        document.write("<br>");
    }
}

// Driven Program
var n = 4;
printTrinomial(n);

</script>

Output:

1 
1 1 1 
1 2 3 2 1 
1 3 6 7 6 3 1