Trigonometry is a branch of mathematics, which deal with the angles, lengths, and heights of triangles and their relationships. It had played an important role to calculate complex functions or large distances which were not possible to calculate without trigonometry. While solving problems with trigonometry, we came across many situations where we have to calculate the trigonometric solutions for the sum of angles or differences of angles. E.g.

Here, 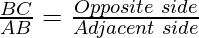
Which is a tangent trigonometric ratio, with an angle opposite to BC.
tan(θ+Φ) = 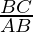
If θ = 30° and Φ = 45°. We know the trigonometric angles of 45° and 30°, but we don’t know the trigonometric angle of (45° + 30° = 75°). So, to simplify these types of problems. We will get to learn trigonometric formulae or identities of sum and differences of two angles which will make things easier.
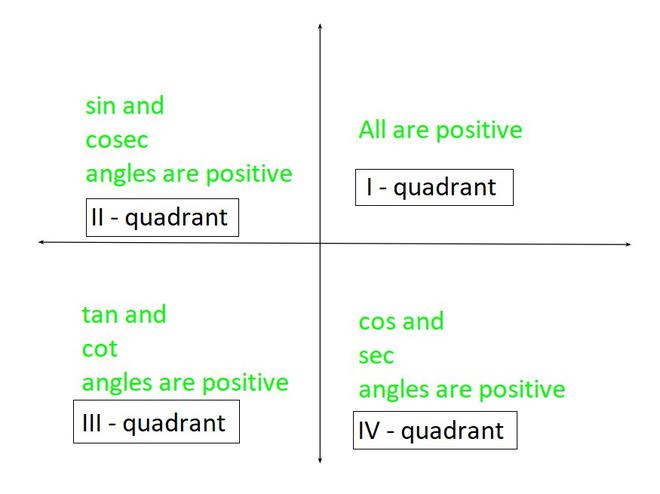
Before moving further first we will see the signs of the trigonometric functions in the four quadrants. These signs play an important role in trigonometry.
Trigonometric identities
Now we are going to find the trigonometric identities. As we know that
sin(-x) = – sin x
cos(-x) = cos x
Because only cos and sec are positive in the fourth quadrant. So, now we prove some results regarding sum and difference of angles:
Let’s consider a unit circle (having radius as 1) with centre at the origin. Let x be the ∠DOA and y be the ∠AOB. Then (x + y) is the ∠DOB. Also let (– y) be the ∠DOC.
Therefore, the coordinates of A, B, C and D are
A = (cos x, sin x)
B = [cos (x + y), sin (x + y)]
C = [cos (– y), sin (– y)]
D = (1, 0).

As, ∠AOB = ∠COD
Adding, ∠BOC both side, we get
∠AOB + ∠BOC = ∠COD + ∠BOC
∠AOC = ∠BOD
In △ AOC and △ BOD
OA = OB (radius of circle)
∠AOC = ∠BOD (Proved earlier)
OC = OD (radius of circle)
△ AOC ≅ △ BOD by SAS congruency.
By using distance formula, for
AC2 = [cos x – cos (– y)]2 + [sin x – sin(–y]2
AC2 = 2 – 2 (cos x cos y – sin x sin y) …………….(i)
And, now
Similarly, using distance formula, we get
BD2 = [1 – cos (x + y)]2 + [0 – sin (x + y)]2
BD2 = 2 – 2 cos (x + y) …………….(ii)
As, △ AOC ≅ △ BOD
AC = BD, So AC2 = BD2
From eq(i) and eq(ii), we get
2 – 2 (cos x cos y – sin x sin y) = 2 – 2 cos (x + y)
So,
cos (x + y) = cos x cos y – sin x sin y
Take y = -y, we get
cos (x + (-y)) = cos x cos (-y) – sin x sin (-y)
cos (x – y) = cos x cos y + sin x sin y
Now, taking
cos (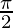 -(x + y)) = cos ((
-(x + y)) = cos ((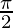 -x) – y) (cos (
-x) – y) (cos (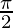 -θ) = sin θ)
-θ) = sin θ)
sin (x – y) = sin x cos y – cos x sin y
take y = -y, we get
sin (x – (-y)) = sin x cos (-y) – cos x sin (-y)
sin (x + y) = sin x cos y + cos x sin y
The derived formulae for trigonometric ratios of compound angles are as follows:
sin (A + B) = sin A cos B + cos A sin B ………………..(1)
sin (A – B) = sin A cos B – cos A sin B ………………..(2)
cos (A + B) = cos A cos B – sin A sin B ..………………(3)
cos (A – B) = cos A cos B + sin A sin B ………………..(4)
By using these formulae, we can obtain some important and mostly used form:
(1) Take, A = 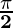
In eq(1) and (3), we get
sin (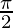 +B) = cos B
+B) = cos B
cos (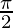 +B) = – sin A
+B) = – sin A
(2) Take, A = π
In eq(1), (2), (3) and (4) we get
sin (π + B) = – sin B
sin (π – B) = sin B
cos (π ± B) = – cos B
(3) Take, A = 2π
In eq(2) and (4) we get
sin (2π – B) = – sin B
cos (2π – B) = cos B
Similarly for cot A, tan A, sec A, and cosec A
(4) 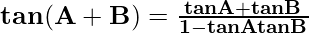
Here, A, B, and (A + B) is not an odd multiple of π/2, so, cosA, cosB and cos(A + B) are non-zero
tan(A + B) = sin(A + B)/cos(A + B)
From eq(1) and (3), we get
tan(A + B) = sin A cos B + cos A sin B/cos A cos B – sin A sin B
Now divide the numerator and denominator by cos A cos B we get
tan(A + B) = 
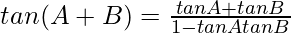
(5) 
As we know that
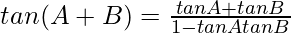
So, on putting B = -B, we get
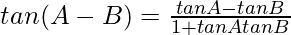
(6) 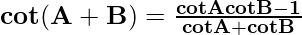
Here, A, B, and (A + B) is not a multiple of π, so, sinA, sinB and sin(A + B) are non-zero
cot(A + B) = cos(A + B)/sin(A + B)
From eq(1) and (3), we get
cot(A + B) = cos A cos B – sin A sin B/sin A cos B + cos A sin B
Now divide the numerator and denominator by sin A sin B we get
cot(A + B) = 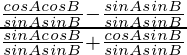
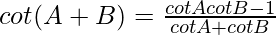
(7) 
As we know that
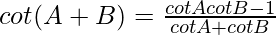
So, on putting B = -B, we get

Here, we will establish two sets of transformation formulae: Factorization and Defactorization formulae.
Defactorization Formulae
In trigonometry, defactorisation means converting a product into a sum or difference. The defactorization formulae are:
(1) 2 sin A cos B = sin (A + B) + sin (A – B)
Proof:
As we know that
sin (A + B) = sin A cos B + cos A sin B ………………………(1)
sin (A – B) = sin A cos B – cos A sin B ………………………(2)
By adding eq(1) and (2), we get
2 sin A cos B = sin (A + B) + sin (A – B)
(2) 2 cos A sin B = sin (A + B) – sin (A – B)
Proof:
As we know that
sin (A + B) = sin A cos B + cos A sin B ………………………(1)
sin (A – B) = sin A cos B – cos A sin B ………………………(2)
By subtracting eq(2) from (1), we get
2 cos A sin B = sin (A + B) – sin (A – B)
(3) 2 cos A cos B = cos (A + B) + cos (A – B)
Proof:
As we know that
cos (A + B) = cos A cos B – sin A sin B ………………………(1)
cos (A – B) = cos A cos B + sin A sin B ………………………(2)
By adding eq(1) and (2), we get
2 cos A cos B = cos (A + B) + cos (A – B)
(4) 2 sin A sin B = cos (A – B) – cos (A + B)
Proof:
cos (A + B) = cos A cos B – sin A sin B ………………………(1)
cos (A – B) = cos A cos B + sin A sin B ………………………(2)
By subtracting eq(3) from (4), we get
2 sin A sin B = cos (A – B) – cos (A + B)
Example 1. Convert each of the following products into the sum or difference.
(i) 2 sin 40° cos 30°
(ii) 2 sin 75° sin 15°
(iii) cos 75° cos 15°
Solution:
(i) Given: A = 40° and B = 30°
Now put all these values in the formula,
2 sin A cos B = sin (A + B) + sin (A – B)
We get
2 sin 40° cos 30° = sin (40 + 30) + sin (40 – 30)
= sin (70°) + sin (10°)
(ii) Given: A = 75° and B = 15°
Now put all these values in the formula,
2 sin A sin B = cos (A – B) – cos (A + B)
We get
2 sin 75° sin 15° = cos (75-15) – cos (75+15)
= cos (60°) – cos (90°)
(iii) Given: A = 75° and B = 15°
Now put all these values in the formula,
2 cos A cos B = cos (A + B) + cos (A – B)
We get
cos 75° cos 15° = 1/2(cos (75+15) + cos (75-15))
= 1/2 (cos (90°) + cos (60°))
Example 2. Solve for 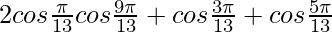
Solution:
Using the formula
2 cos A cos B = cos (A + B) + cos (A – B)

= 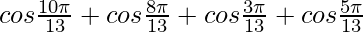
= 
= 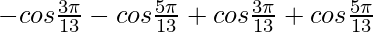
Hence,
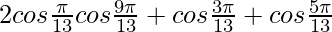 = 0
= 0
Factorisation Formulae
In trigonometry, factorisation means converting sum or difference into the product. The factorisation formulae are:
(1) sin (C) + sin (D) = 2 sin 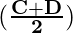 cos
cos 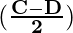
Proof:
We have
2 sin A cos B = sin (A + B) + sin (A – B) ………………………(1)
So now, we are taking
A + B = C and A – B = D
Then, A =  and B =
and B = 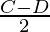
Now put all these values in eq(1), we get
2 sin ( ) cos (
) cos ( ) = sin (C) + sin (D)
) = sin (C) + sin (D)
Or
sin (C) + sin (D) = 2 sin ( ) cos (
) cos ( )
)
(2) sin (C) – sin (D) = 2 cos 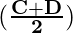 sin
sin 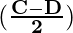
Proof:
We have
2 cos A sin B = sin (A + B) – sin (A – B) ………………………(1)
So now, we are taking
A + B = C and A – B = D
Then, A =  and B =
and B = 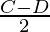
Now put all these values in eq(1), we get
2 cos ( ) sin (
) sin ( ) = sin (C) – sin (D)
) = sin (C) – sin (D)
Or
sin (C) – sin (D) = 2 cos ( ) sin (
) sin ( )
)
(3) cos (C) + cos (D) = 2 cos 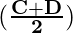 cos
cos 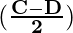
Proof:
We have
2 cos A cos B = cos (A + B) + cos (A – B) ………………………(1)
So now, we are taking
A + B = C and A – B = D
Then, A =  and B =
and B = 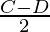
Now put all these values in eq(1), we get
2 cos ( ) cos (
) cos ( ) = cos (C) + cos (D)
) = cos (C) + cos (D)
Or
cos (C) + cos (D) = 2 cos ( ) cos (
) cos ( )
)
(4) cos (C) – cos (D) = 2 sin 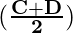 sin
sin 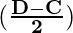
Proof:
We have
2 sin A sin B = cos (A – B) – cos (A + B) ………………………(1)
So now, we are taking
A + B = C and A – B = D
Then, A =  and B =
and B = 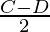
Now put all these values in eq(1), we get
2 sin ( ) sin (
) sin ( ) = cos (C) – cos (D)
) = cos (C) – cos (D)
Or
cos (C) – cos (D) = 2 sin ( ) sin (
) sin ( )
)
Explain 1. Express each of the following as a product
(i) sin 40° + sin 20°
(ii) sin 60° – sin 20°
(iii) cos 40° + cos 80°
Solution:
(i) Given: C = 40° and D = 20°
Now put all these values in the formula,
sin (C) + sin (D) = 2 sin 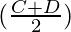 cos
cos 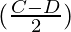
We get
sin 40° + sin 20° = 2 sin 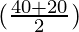 cos
cos 
= 2 sin 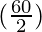 cos
cos 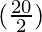
= 2 sin 30° cos 10°
(ii) Given: C = 60° and D = 20°
Now put all these values in the formula,
sin (C) – sin (D) = 2 cos 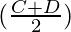 sin
sin 
We get
sin 60° – sin 20° = 2 cos 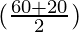 sin
sin 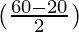
= 2 cos 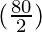 sin
sin 
= 2 cos 40° sin 20°
(iii) Given: C = 80° and D = 40°
Now put all these values in the formula,
cos (C) + cos (D) = 2 cos 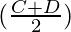 cos
cos 
We get
cos 40° + cos 80° = 2 cos 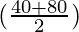 cos
cos 
= 2 cos 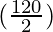 cos
cos 
= 2 cos 60° cos 20°
Example 2. Prove that: 1 + cos 2x + cos 4x + cos 6x = 4 cos x cos 2x cos 3x
Solution:
Lets take LHS
1 + cos 2x + cos 4x + cos 6x
Here, cos 0x = 1
So,
(cos 0x + cos 2x) + (cos 4x + cos 6x)
Using formula
cos (C) + cos (D) = 2 cos 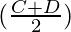 cos
cos 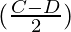
We get
(2 cos 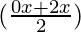 cos
cos 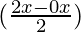 ) + (2 cos
) + (2 cos 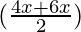 cos
cos 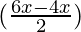 )
)
(2 cos x cos x) + (2 cos 5x cos x)
Taking 2 cos x common, we have
2 cos x (cos x + cos 5x)
Again using the formula
cos (C) + cos (D) = 2 cos 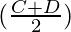 cos
cos 
We get
2 cos x (2 cos 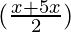 cos
cos  )
)
2 cos x (2 cos 3x cos 2x)
4 cos x cos 2x cos 3x
LHS = RHS
Hence proved
Trigonometric ratios of multiple angles (2A) in terms of angle A
The trigonometric ratios of an angle in a right triangle define the relationship between the angle and the length of its sides. sin 2x or cos 2x, etc. are also, one such trigonometrical formula, also known as double angle formula, as it has a double angle in it.
(1) sin 2A = 2 sin A cos A
Proof:
As we know that
sin (A + B) = sin A cos B + cos A sin B ………………..(1)
Now taking B = A, in eq(1), we get
sin (A + A) = sin A cos A + cos A sin A
sin 2A = 2 sin A cos A
(2) cos 2A = cos2 A – sin2 A
Proof:
As we know that
cos (A + B) = cos A cos B – sin A sin B ………………..(1)
Now taking B = A, in eq(1), we get
cos (A + A) = cos A cos A + sin A sin A
cos 2A = cos2 A – sin2 A
(3) cos 2A = 2cos2 A – 1
Proof:
As we know that
cos 2A = cos2 A – sin2 A ………………..(1)
We also know that
sin2 A + cos2 A = 1
So, sin2 A = 1 – cos2 A
Now put the value of sin2 A in eq(1), we get
cos 2A = cos2 A – (1 – cos2 A)
cos 2A = cos2 A – 1 + cos2 A
cos 2A = 2cos2 A – 1
(4) cos 2A = 1 – 2sin2 A
Proof:
As we know that
cos 2A = 2cos2 A – 1 ………………..(1)
We also know that
sin2 A + cos2 A = 1
So, cos2 A = 1 – sin2 A
Now put the value of sin2 A in eq(1), we get
cos 2A = 2(1 – sin2 A) – 1
cos 2A = 2 – 2sin2 A) – 1
cos 2A = 1 – 2sin2 A
(5) cos 2A = 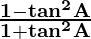
Proof:
As we know that
cos 2A = cos2 A – sin2 A
So, now dividing, by sin2 A + cos2 A = 1, we get
cos 2A = 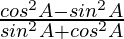
Again dividing the numerator and denominator by cos2 A, we get
cos 2A = 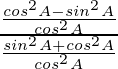
cos 2A = 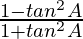
(6) sin 2A = 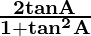
Proof:
As we know that
sin (A + B) = sin A cos B + cos A sin B ………………..(1)
Now taking B = A, in eq(1), we get
sin (A + A) = sin A cos A + cos A sin A
sin 2A = 2 sin A cos A
As we also know that sin2 A + cos2 A = 1
So, now dividing, by sin2 A + cos2 A = 1, we get
sin 2A = 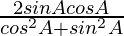
Now, on dividing the numerator and denominator by cos2 A, we get
sin 2A = 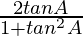
(7) tan 2A = 
Proof:
As we know that
 ………………..(1)
………………..(1)
Now taking B = A, in eq(1), we get
tan(A + A) = 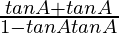
tan 2A = 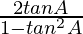
Example: Prove that
(i) 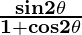 = tan θ
= tan θ
(ii) 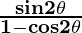 = cot θ
= cot θ
(iii) cos 4x = 1 – 8 sin2x cos2x
Solution:
(i) sin 2θ = 2 sin θ cos θ ………..(from identity 1)
and, 1 + cos 2θ = 2cos2θ ………..(from identity 3)
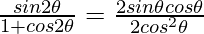
= 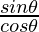
= tan θ
Hence Proved
(ii) sin 2θ = 2 sin θ cos θ ………..(from identity 1)
and, 1 – cos 2θ = 2sin2θ ………..(from identity 4)
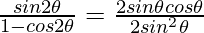
= 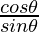
= cot θ
Hence Proved
(iii) cos 4x = cos 2(2x)
= 1 – 2sin2(2x) (using 16)
= 1 – 2(sin(2x))2
= 1 – 2(2 sin x cos x)2 (using identity 1)
= 1 – 2(4 sin2 x cos2 x)
cos 4x = 1 – 8 sin2 x cos2 x
Hence Proved
Trigonometric ratios of multiple angles (3A) in terms of angle A
The trigonometric ratios of an angle in a right triangle define the relationship between the angle and the length of its sides. sin 3x or cos 3x, etc. are also, one such trigonometrical formula, also known as triple angle formula, as it has a triple angle in it.
(1) sin 3A = 3sin A – 4 sin3A
Proof:
Let’s take LHS
sin 3A = sin(2A + A)
Using identity
sin (A + B) = sin A cos B + cos A sin B
We get
sin 3A = sin 2A cos A + cos 2A sin A
= 2sin A cos A cos A + (1 – 2 sin2A)sin A
= 2sin A(1 – sin2A) + sin A – 2 sin3A
= 2sin A – 2sin3A + sin A – 2 sin3A
sin 3A = 3sin A – 4 sin3A
(2) cos 3A = 4 cos3A – 3cos A
Proof:
Let’s take LHS
sin 3A = sin(2A + A)
Using identity
cos (A + B) = cos A cos B – sin A sin B
We get
cos 3A = cos 2A cos A – sin 2A sin A
= (2cos2A – 1)cos A – 2sin A cos A sin A
= (2cos2A – 1)cos A – 2cos A(1 – cos2A)
= 2cos3A – cos A – 2cos A + 2cos3A)
cos 3A = 4 cos3A – 3cos A
(3) tan 3A = 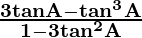
Proof:
Let’s take LHS
tan 3A = tan(2A + A)
Using identity
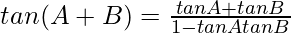
We get
tan 3A = 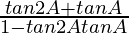
= 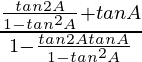
= 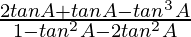
= 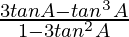
Example 1. Solve 2sin3xsinx.
Solution:
We have 2sin3xsinx
We also write as y = y1 . y2 ….(1)
Here, y1 = 2sin3x
y2 = sinx
So let’s solve y1 = 2sin3x
Using identity
sin 3A = 3sin A – 4 sin3A
We get
y1 = 2(sin x – 4 sin3x)
= 2sin x – 8 sin3x
Now put these values in eq(1), we get
y = (2sin x – 8 sin3x)(sinx)
= 2sin2 x – 8 sin4x
Example 2. Solve 2tan3xtanx.
Solution:
We have 2tan3xtanx
We also write as y = y1 . y2 ….(1)
Here, y1 = 2tan3x
y2 = tanx
So let’s solve y1 = 2tan3x
Using identity
tan 3A = 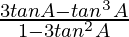
We get
y1 = 2(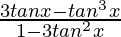 )
)
= 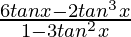
Now put these values in eq(1), we get
y = (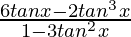 )(tanx)
)(tanx)
= 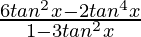
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...