Tree Entropy in R Programming
Last Updated :
25 Aug, 2020
Entropy in R Programming is said to be a measure of the contaminant or ambiguity existing in the data. It is a deciding constituent while splitting the data through a decision tree. An unsplit sample has an entropy equal to zero while a sample with equally split parts has entropy equal to one. Two major factors that are considered while choosing an appropriate tree are- information gain (IG) and entropy.
Formula :
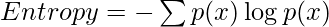
where, p(x) is the probability
For example, consider a school data set of a decision tree whose entropy needs to be calculated.
| Library available | Coaching joined | Parent’s education | Student’s performance |
|---|
| yes | yes | uneducated | bad |
| yes | no | uneducated | bad |
| no | no | educated | good |
| no | no | uneducated | bad |
Hence, it is clearly seen that a student’s performance is affected by three factors – library available, coaching joined, and parent’s education. A decision tree can be constructed using the information of these three variables for the prediction of student’s performance and hence are called predictor variables. The variables with more information are considered a better splitter of the decision tree.
So to calculate the entropy of parent node – Student’s performance, the above entropy formula is used but probability needs to be calculated first.
There are four values in the Student’s performance column out of which two performances are good and two are bad.

Hence, total entropy of parent can be calculated as below
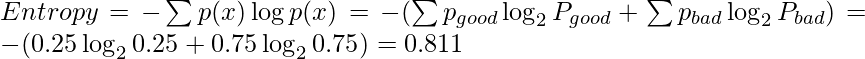
Information Gain using Entropy
Information gain is a parameter used to decide the best variable available for splitting the data at every node in the decision tree. So IG of every predictor variable can be calculated and the variable with the highest IG wins the race of deciding factor for splitting of root nodes.
Formula:
Information Gain(IG) = Entropyparent – (weighted average * Entropychildren)
Now to calculate IG of the predictor variable coaching joined, firstly split the parent node according to this variable.
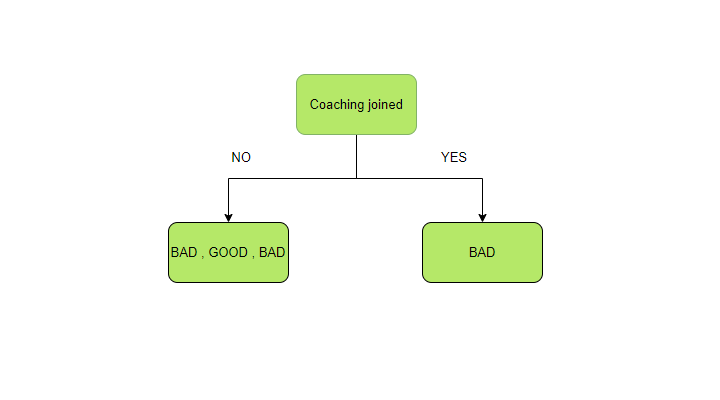
Now there are two parts and their entropy is first calculated individually.
The entropy of the left part
There are two types of output available – good and bad. On the left part, there are three total outcomes with two being bad and one being good. Hence, Pgood and Pbad is calculated again as follows:

The entropy of the right part
There is only one component in right, ie, bad performance. Hence, the probability becomes one. And the entropy becomes 0 because there is only one category to which output can belong to.
Calculating the weighted average with Entropy of children

There are 3 outcomes in left child node and 1 in the right node. While, Entropyleft node has been calculated as 0.9 and Entropyright node is 0.
Now keeping the values in the formula above we get a weighted average for this example:
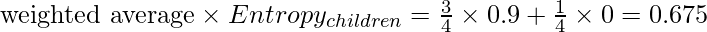
Calculating IG
Now putting the calculated weighted average in IG formula simply to obtain IG of ‘coaching joined’.
IG(coaching joined) = Entropyparent - (weighted average * Entropychildren)
IG(coaching joined) = 0.811 - 0.675 = 0.136
Using the same steps and formula IG of other predictor variables is calculated, compared, and variable with the highest IG is therefore selected for splitting the data at every node.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...