Transportation Problem | Set 5 ( Unbalanced )

An introduction to the transportation problem has been discussed in this article. In this article, the method to solve the unbalanced transportation problem will be discussed.

Below transportation problem is an unbalanced transportation problem.

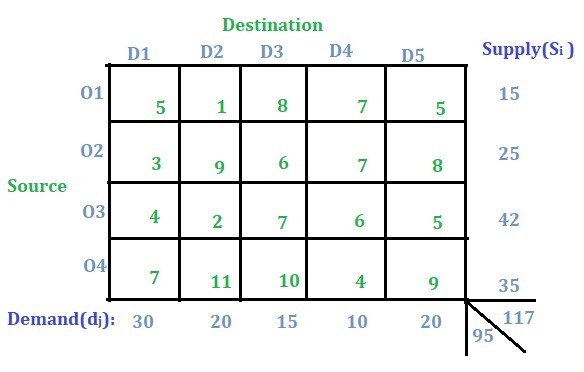
The problem is unbalanced because the sum of all the supplies i.e. O1, O2, O3 and O4 is not equal to the sum of all the demands i.e. D1, D2, D3, D4 and D5.

Solution:
In this type of problem, the concept of a dummy row or a dummy column will be used. As in this case, since the supply is more than the demand so a dummy demand column will be added and a demand of (total supply – total demand) will be given to that column i.e. 117 – 95 = 22 as shown in the image below. If demand were more than the supply then a dummy supply row would have been added.

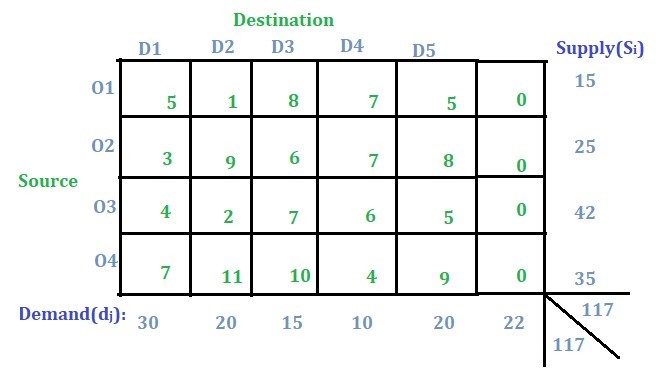
Now that the problem has been updated to a balanced transportation problem, it can be solved using any one of the following methods to solve a balanced transportation problem as discussed in the earlier posts:

1. NorthWest Corner Method
2. Least Cost Cell Method
3. Vogel’s Approximation Method

My Personal Notes arrow_drop_up

Save