Total time required to travel a path denoted by a given string
Last Updated :
28 Jun, 2021
Given a string path consisting of characters ‘N’, ‘S’, ‘E’ and ‘W’ denoting 1 unit movement in North, South, East, and West directions respectively, the task is to find the time taken to travel the complete path starting from the origin, if it takes 2 and 1 minutes to travel on an unvisited and visited segment respectively.
Examples :
Input: path = “NNES”
Output : 8

Explanation: Since every segment is visited only once, cost = 2 * 4 = 8.
Input : path = “NSE”
Output : 5
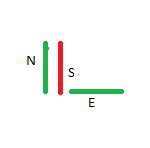
Explanation:
Step 1: Travel north. Time Taken = 2 minutes.
Step 2: Travel south on that same visited segment. Time Taken = 1 minutes.
Step 3: Travel east.Time Taken = 2 minutes. Therefore, total time taken = 2 + 1 + 2 = 5.
Approach: The idea is to use a Set to store all the visited segments and before visiting each segment, check if it is present in the Set or not. Follow the steps below to solve the problem.
- Initialize a set s to store a pair of integers. The set will store all visited segments.
- Initialize two integers x = 0 and y = 0 denoting the current position. Also, initialize a variable time = 0 to store the total time needed to travel the complete path.
- Traverse the string and follow the below steps
- Initialize two integers p and q to x and y respectively.
- If path[i] is equal to ‘N’ increment y, else if path[i] is equal to ‘S’ decrement y, else if path[i] is equal to ‘E’ increment x, otherwise decrement x.
- Check if the segment {p+x, q+y} exists in the set or not. if it does add 1 to the value of time otherwise add 2 to the value of time.
- Insert the segment {p+x, q+y} into the set.
- After completing the above steps print the value of time.
Below is implementation of the above approach.
C++
#include <bits/stdc++.h>
using namespace std;
void calcTotalTime(string path)
{
int time = 0;
int x = 0, y = 0;
set<pair<int, int> > s;
for (int i = 0; i < path.size(); i++) {
int p = x;
int q = y;
if (path[i] == 'N')
y++;
else if (path[i] == 'S')
y--;
else if (path[i] == 'E')
x++;
else if (path[i] == 'W')
x--;
if (s.find({ p + x, q + y })
== s.end()) {
time += 2;
s.insert({ p + x, q + y });
}
else
time += 1;
}
cout << time << endl;
}
int main()
{
string path = "NSE";
calcTotalTime(path);
return 0;
}
|
Java
import java.util.*;
class GFG{
static void calcTotalTime(String path)
{
int time = 0;
int x = 0, y = 0;
Set<String> s = new HashSet<>();
for(int i = 0; i < path.length(); i++)
{
int p = x;
int q = y;
if (path.charAt(i) == 'N')
y++;
else if (path.charAt(i) == 'S')
y--;
else if (path.charAt(i) == 'E')
x++;
else if (path.charAt(i) == 'W')
x--;
String o = (p + x) + " " + (q + y);
if (!s.contains(o))
{
time += 2;
s.add(o);
}
else
time += 1;
}
System.out.println(time);
}
public static void main(String[] args)
{
String path = "NSE";
calcTotalTime(path);
}
}
|
Python3
def calcTotalTime(path):
time = 0
x = 0
y = 0
s = set([])
for i in range(len(path)):
p = x
q = y
if (path[i] == 'N'):
y += 1
elif (path[i] == 'S'):
y -= 1
elif (path[i] == 'E'):
x += 1
elif (path[i] == 'W'):
x -= 1
if (p + x, q + y) not in s:
time += 2
s.add((p + x, q + y))
else:
time += 1
print(time)
if __name__ == "__main__":
path = "NSE"
calcTotalTime(path)
|
C#
using System;
using System.Collections.Generic;
class GFG{
static void calcTotalTime(string path)
{
int time = 0;
int x = 0, y = 0;
HashSet<string> s = new HashSet<string>();
for(int i = 0; i < path.Length; i++)
{
int p = x;
int q = y;
if (path[i] == 'N')
y++;
else if (path[i] == 'S')
y--;
else if (path[i] == 'E')
x++;
else if (path[i] == 'W')
x--;
string o = (p + x) + " " + (q + y);
if (s.Contains(o) == false)
{
time += 2;
s.Add(o);
}
else
time += 1;
}
Console.Write(time);
}
public static void Main()
{
string path = "NSE";
calcTotalTime(path);
}
}
|
Javascript
<script>
function calcTotalTime(path)
{
var time = 0;
var x = 0, y = 0;
var s = new Set();
for(var i = 0; i < path.length; i++)
{
var p = x;
var q = y;
if (path[i] == 'N')
y++;
else if (path[i] == 'S')
y--;
else if (path[i] == 'E')
x++;
else if (path[i] == 'W')
x--;
if (!s.has([p + x, q + y].toString()))
{
time += 2;
s.add([p + x, q + y].toString());
}
else
time += 1;
}
document.write(time)
}
var path = "NSE";
calcTotalTime(path);
</script>
|
Time Complexity: O(NlogN)
Auxiliary Space: O(N)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...