Total position where king can reach on a chessboard in exactly M moves
Last Updated :
23 Jun, 2022
Given an integer M, an 8 * 8 chessboard and the king is placed on one of the square of the chessboard. Let the coordinate of the king be (R, C).
Note that the king can move to a square whose coordinate is (R1, C1) if and only if below condition is satisfied.
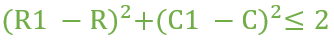
The task is to count the number of position where the king can reach (excluding the initial position) from the given square in exactly M moves.
Examples:
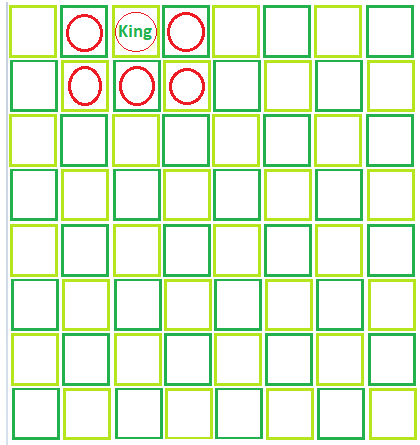
Input: row = 1, column = 3, moves = 1
Output: Total number of position where king can reached = 5
Input: row = 2, column = 5, moves = 2
Output: Total number of position where king can reached = 19
Approach: Calculate the coordinates of the top left square that can be visited by the king (a, b) and the coordinates of the bottom right square (c, d) of the chessboard that the king can visit. Then the total number of cells that the king can visit will be (c – a + 1) * (d – b + 1) – 1.
Below is the implementation of the above approach:
C++
#include <iostream>
using namespace std;
int Square(int row, int column, int moves)
{
int a = 0, b = 0, c = 0, d = 0, total = 0;
a = row - moves;
b = row + moves;
c = column - moves;
d = column + moves;
if (a < 1)
a = 1;
if (c < 1)
c = 1;
if (b > 8)
b = 8;
if (d > 8)
d = 8;
total = (b - a + 1) * (d - c + 1) - 1;
return total;
}
int main()
{
int R = 4, C = 5, M = 2;
cout << Square(R, C, M);
return 0;
}
|
Java
class GFG
{
static int Square(int row, int column,
int moves)
{
int a = 0, b = 0, c = 0,
d = 0, total = 0;
a = row - moves;
b = row + moves;
c = column - moves;
d = column + moves;
if (a < 1)
a = 1;
if (c < 1)
c = 1;
if (b > 8)
b = 8;
if (d > 8)
d = 8;
total = (b - a + 1) * (d - c + 1) - 1;
return total;
}
public static void main(String []args)
{
int R = 4, C = 5, M = 2;
System.out.println(Square(R, C, M));
}
}
|
Python3
def Square(row, column, moves) :
a = 0; b = 0; c = 0;
d = 0; total = 0;
a = row - moves;
b = row + moves;
c = column - moves;
d = column + moves;
if (a < 1) :
a = 1;
if (c < 1) :
c = 1;
if (b > 8) :
b = 8;
if (d > 8) :
d = 8;
total = (b - a + 1) * (d - c + 1) - 1;
return total;
if __name__ == "__main__" :
R = 4; C = 5; M = 2;
print(Square(R, C, M));
|
C#
using System;
class GFG
{
static int Square(int row, int column,
int moves)
{
int a = 0, b = 0, c = 0,
d = 0, total = 0;
a = row - moves;
b = row + moves;
c = column - moves;
d = column + moves;
if (a < 1)
a = 1;
if (c < 1)
c = 1;
if (b > 8)
b = 8;
if (d > 8)
d = 8;
total = (b - a + 1) * (d - c + 1) - 1;
return total;
}
public static void Main()
{
int R = 4, C = 5, M = 2;
Console.Write(Square(R, C, M));
}
}
|
PHP
<?php
function Square($row, $column, $moves)
{
$a = 0; $b = 0; $c = 0;
$d = 0; $total = 0;
$a = $row - $moves;
$b = $row + $moves;
$c = $column - $moves;
$d = $column + $moves;
if ($a < 1)
$a = 1;
if ($c < 1)
$c = 1;
if ($b > 8)
$b = 8;
if ($d > 8)
$d = 8;
$total = ($b - $a + 1) *
($d - $c + 1) - 1;
return $total;
}
$R = 4; $C = 5; $M = 2;
echo Square($R, $C, $M);
?>
|
Javascript
<script>
function Square(row, column, moves)
{
var a = 0, b = 0, c = 0, d = 0, total = 0;
a = row - moves;
b = row + moves;
c = column - moves;
d = column + moves;
if (a < 1)
a = 1;
if (c < 1)
c = 1;
if (b > 8)
b = 8;
if (d > 8)
d = 8;
total = (b - a + 1) * (d - c + 1) - 1;
return total;
}
var R = 4, C = 5, M = 2;
document.write( Square(R, C, M));
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...