Total number Of valid Home delivery arrangements
Last Updated :
22 Sep, 2023
Given the number of orders, find the number of valid arrangements of orders where delivery of ith order is always after the pickup of ith order.
Examples:
Input: N = 1
Output: 1
Here, the total event is 2. They are {P1, D1}.
The total possible arrangement is 2! = 2. [P1, D1] and [D1, P1].
So the only valid arrangement possible: [P1, D1].
[D1, P1] is an invalid arrangement as delivery of 1st order is done before pickup of 1st order.
Input: N = 2
Output: 6
Here, the total event is 4. They are {P1, D1, P2, D2}.
Here, the total possible arrangements are 4! = 24.
Among them, 6 are valid arrangements:
[P1, P2, D1, D2], [P1, D1, P2, D2], [P1, P2, D2, D1], [P2, P1, D2, D1], [P2, P1, D1, D2], and [P2, D2, P1, D1].
The rest of all are invalid arrangements.
Some invalid arrangements:
[P1, D1, D2, P2] – Delivery of 2nd order is done before pickup
[P2, D1, P1, D2] – Delivery of 1st order is done before pickup
[D1, D2, P2, P1] – Delivery of both orders is before pickup
Approach 1:
- Consider N = 4, we have a total of 8 events.
- There are 4 events for pickup {P1, P2, P3, P4} and 4 events for delivery {D1, D2, D3, D4}.
- If we consider only pickup events, there are no restrictions on arrangements between pickups. So, total possible arrangements 4!
- Now we consider delivery. We start from the last pickup we made.
- For D4, we can place D4 only after P4.
That is P1, P2, P3, P4, __. So there is only 1 valid position. - For D3, we can place D3 in any one of the following positions.
They are P1, P2, P3, __, P4, __, D4, __. So there are 3 valid positions. - For D2, we can place D2 in any one of the following positions.
They are P1, P2, __, P3, __, P4, __, D4, __, D3 __ .So 5 valid positions. - For D1, we can place D1 in any one of the following positions.
They are P1, __, P2, __, P3, __, P4, __, D4, __, D3 __, D2, __ .So, 7 valid positions.
For any N, total valid arrangements:
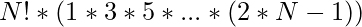
Below is the implementation of the above approach.
C++
#include <bits/stdc++.h>
using namespace std;
int Arrangements(int N)
{
int result = 1;
for(int i = 1; i <= N; i++)
{
result = result * i * (2 * i - 1);
}
return result;
}
int main()
{
int N = 4;
cout << Arrangements(N);
return 0;
}
|
Java
class GFG{
public static int Arrangements(int N)
{
int result = 1;
for(int i = 1; i <= N; i++)
{
result = result * i * (2 * i - 1);
}
return result;
}
public static void main(String[] args)
{
int N = 4;
System.out.print(Arrangements(N));
}
}
|
Python3
def Arrangements(N):
result = 1
for i in range(1, N + 1):
result = result * i * (2 * i - 1)
return result
N = 4;
print(Arrangements(N));
|
C#
using System;
class GFG{
public static int Arrangements(int N)
{
int result = 1;
for(int i = 1; i <= N; i++)
{
result = result * i * (2 * i - 1);
}
return result;
}
public static void Main(String[] args)
{
int N = 4;
Console.Write(Arrangements(N));
}
}
|
Javascript
<script>
function Arrangements(N)
{
let result = 1;
for(let i = 1; i <= N; i++)
{
result = result * i * (2 * i - 1);
}
return result;
}
let N = 4;
document.write(Arrangements(N));
</script>
|
Time Complexity: O(N)
Auxiliary Space: O(1)
Approach 2:
- For N number of orders, we have
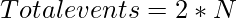
- So the total number of arrangements possible is
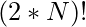
- Now, each order can only be valid if delivery is done after pickup.
For each [Pi, Di], we can’t change this arrangement, ie we can’t do [Di, Pi]. There is only one valid arrangement for each such order. So we need to divide by 2 for each order. So the total valid arrangement is 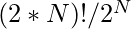
Below is the implementation of the above approach.
C++
#include <bits/stdc++.h>
using namespace std;
int Arrangements(int N)
{
int result = 1;
for (int i = 1; i <= 2 * N; i += 2)
result = (result * i * (i + 1)) / 2;
return result;
}
int main()
{
int N = 4;
cout << Arrangements(N);
return 0;
}
|
Java
import java.util.*;
class GFG{
public static int Arrangements(int N)
{
int result = 1;
for (int i = 1; i <= 2 * N; i += 2)
result = (result * i * (i + 1)) / 2;
return result;
}
public static void main(String args[])
{
int N = 4;
System.out.print(Arrangements(N));
}
}
|
Python3
def Arrangements(N):
result = 1;
for i in range(1, (2 * N) + 1, 2):
result = (result * i * (i + 1)) / 2;
return int(result);
if __name__ == '__main__':
N = 4;
print(Arrangements(N));
|
C#
using System;
class GFG{
public static int Arrangements(int N)
{
int result = 1;
for (int i = 1; i <= 2 * N; i += 2)
result = (result * i * (i + 1)) / 2;
return result;
}
public static void Main()
{
int N = 4;
Console.Write(Arrangements(N));
}
}
|
Javascript
<script>
function Arrangements(N)
{
var result = 1;
for (var i = 1; i <= 2 * N; i += 2)
result = parseInt( (result * i * (i + 1)) / 2);
return result;
}
var N = 4;
document.write( Arrangements(N));
</script>
|
Time complexity: O(N)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...