Total number of possible Binary Search Trees using Catalan Number
Last Updated :
16 Jun, 2022
Given an integer N, the task is to count the number of possible Binary Search Trees with N keys.
Examples:
Input: N = 2
Output: 2
For N = 2, there are 2 unique BSTs
1 2
\ /
2 1
Input: N = 9
Output: 4862
Approach: The number of binary search trees that will be formed with N keys can be calculated by simply evaluating the corresponding number in Catalan Number series.
First few Catalan numbers for n = 0, 1, 2, 3, … are 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, …
Catalan numbers satisfy the following recursive formula:
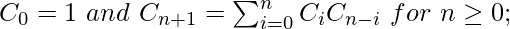
Below is the implementation of the above approach:
C++
#include <iostream>
using namespace std;
int uniqueBSTs(int n)
{
int n1, n2, sum = 0;
if (n == 1 || n == 0)
return 1;
for (int i = 1; i <= n; i++) {
n1 = uniqueBSTs(i - 1);
n2 = uniqueBSTs(n - i);
sum += n1 * n2;
}
return sum;
}
int main()
{
int n = 2;
cout << uniqueBSTs(n);
return 0;
}
|
Java
import java.io.*;
class GFG {
static int uniqueBSTs(int n)
{
int n1, n2, sum = 0;
if (n == 1 || n == 0)
return 1;
for (int i = 1; i <= n; i++) {
n1 = uniqueBSTs(i - 1);
n2 = uniqueBSTs(n - i);
sum += n1 * n2;
}
return sum;
}
public static void main(String[] args)
{
int n = 2;
System.out.println(uniqueBSTs(n));
}
}
|
Python3
def uniqueBSTs(n):
n1, n2, sum = 0, 0, 0
if (n == 1 or n == 0):
return 1
for i in range(1, n + 1):
n1 = uniqueBSTs(i - 1)
n2 = uniqueBSTs(n - i)
sum += n1 * n2
return sum
n = 2
print(uniqueBSTs(n))
|
C#
using System;
class GFG {
static int uniqueBSTs(int n)
{
int n1, n2, sum = 0;
if (n == 1 || n == 0)
return 1;
for (int i = 1; i <= n; i++)
{
n1 = uniqueBSTs(i - 1);
n2 = uniqueBSTs(n - i);
sum += n1 * n2;
}
return sum;
}
static public void Main()
{
int n = 2;
Console.WriteLine(uniqueBSTs(n));
}
}
|
Javascript
<script>
function uniqueBSTs(n)
{
let n1, n2, sum = 0;
if (n == 1 || n == 0)
return 1;
for (let i = 1; i <= n; i++)
{
n1 = uniqueBSTs(i - 1);
n2 = uniqueBSTs(n - i);
sum += n1 * n2;
}
return sum;
}
let n = 2;
document.write(uniqueBSTs(n));
</script>
|
The problem can be solved in a dynamic programming way.
Here is a snippet of how the recurrence tree will proceed:
G(4)
/ | | \
G(0)G(3) G(1)G(2) G(2)G(1) G(3)G(0)
/ | \
G(0)G(2) G(1)G(1) G(2)G(0)
/ \
G(0)G(1) G(1)G(0) // base case
Note: Without memoization, the time complexity is upper bounded by O(N x N!).
Given a sequence 1…n, to construct a Binary Search Tree (BST) out of the sequence, we could enumerate each number i in the sequence, and use the number as the root, naturally, the subsequence 1…(i-1) on its left side would lay on the left branch of the root, and similarly the right subsequence (i+1)…n lay on the right branch of the root. We then can construct the subtree from the subsequence recursively. Through the above approach, we could ensure that the BST that we construct is all unique since they have unique roots.
The problem is to calculate the number of unique BST. To do so, we need to define two functions:
1.G(n): the number of unique BST for a
sequence of length n.
2.F(i, n), 1 <= i <= n: The number of unique
BST, where the number i is the root of BST,
and the sequence ranges from 1 to n. As one can
see, G(n) is the actual function we need to calculate
in order to solve the problem. And G(n) can be derived
from F(i, n), which at the end, would recursively refer
to G(n).
First of all, given the above definitions, we can see
that the total number of unique BST G(n), is the sum of
BST F(i) using each number i as a root. i.e.,
G(n) = F(1, n) + F(2, n) + ... + F(n, n).
Given a sequence 1…n, we pick a number i out of the
sequence as the root, then the number of
unique BST with the specified root F(i), is the
cartesian product of the number of BST for
its left and right subtrees.For example, F(2, 4):
the number of unique BST tree with number 2
as its root. To construct an unique BST out of the
entire sequence [1, 2, 3, 4] with 2 as the
root, which is to say, we need to construct an unique
BST out of its left subsequence [1] and another BST out
of the right subsequence [3,4], and then combine them
together (i.e. cartesian
product). F(i, n) = G(i-1) * G(n-i) 1 <= i <= n
Combining the above two formulas, we obtain the
recursive formula for G(n). i.e.
G(n) = G(0) * G(n-1) + G(1) * G(n-2) + … + G(n-1) * G(0)
In terms of calculation, we need to start with the lower number, since the value of G(n)
depends on the values of G(0) … G(n-1).
Below is the above implementation of the above algorithm:
C++
#include <iostream>
using namespace std;
int uniqueBSTs(int n)
{
int dparray[n + 1] = { 0 };
dparray[0] = dparray[1] = 1;
for (int i = 2; i <= n; ++i)
{
for (int k = 1; k <= i; ++k)
{
dparray[i] += dparray[k - 1] * dparray[i - k];
}
}
return dparray[n];
}
int main()
{
int n = 2;
cout << uniqueBSTs(n);
return 0;
}
|
Java
import java.io.*;
import java.util.*;
class GFG
{
static int uniqueBSTs(int n)
{
int[] dparray = new int[n + 1];
Arrays.fill(dparray, 0);
dparray[0] = dparray[1] = 1;
for (int i = 2; i <= n; ++i)
{
for (int k = 1; k <= i; ++k)
{
dparray[i] += dparray[k - 1] * dparray[i - k];
}
}
return dparray[n];
}
public static void main (String[] args)
{
int n = 2;
System.out.println(uniqueBSTs(n));
}
}
|
Python3
def uniqueBSTs(n):
dparray = [0 for i in range(n + 1)]
dparray[0] = 1
dparray[1] = 1
for i in range(2, n + 1, 1):
for k in range(1, i + 1, 1):
dparray[i] += (dparray[k - 1] *
dparray[i - k])
return dparray[n]
if __name__ == '__main__':
n = 2
print(uniqueBSTs(n))
|
C#
using System;
class GFG{
static int uniqueBSTs(int n)
{
int[] dparray = new int[n + 1];
dparray[0] = dparray[1] = 1;
for(int i = 2; i <= n; ++i)
{
for(int k = 1; k <= i; ++k)
{
dparray[i] += dparray[k - 1] *
dparray[i - k];
}
}
return dparray[n];
}
public static void Main(String[] args)
{
int n = 2;
Console.WriteLine(uniqueBSTs(n));
}
}
|
Javascript
<script>
function uniqueBSTs(n)
{
let dparray = new Array(n + 1);
dparray.fill(0);
dparray[0] = dparray[1] = 1;
for (let i = 2; i <= n; ++i)
{
for (let k = 1; k <= i; ++k)
{
dparray[i] += dparray[k - 1] * dparray[i - k];
}
}
return dparray[n];
}
let n = 2;
document.write(uniqueBSTs(n));
</script>
|
Time Complexity: O(N2)
Space Complexity: O(N)
In this post, we will discuss an O(n) and an O(1) space solution based on Dynamic Programming.
We know that the formula for Catalan number for a variable n is 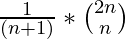 which simplifies to
which simplifies to 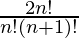
Similarly Catalan number for (n-1) nodes = 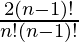
The formula for n nodes can be rewritten as 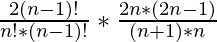
= Catalan number for (n-1) nodes* 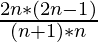
So for every iteration for ‘i’ going from 1 to n we will store catalan number for ‘i-1’ nodes and compute for ith node.
Below is the implementation for the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int numberOfBST(int n)
{
long v = 1;
for (int i = 2; i <= n; i++) {
v = ((v * (i * 2) * (i * 2 - 1)) / ((i + 1) * (i)));
}
return v;
}
int main()
{
int n = 4;
cout << "Number of Unique BST for " << n << " nodes is "
<< numberOfBST(n) << endl;
return 0;
}
|
Java
class GFG{
static long numberOfBST(int n)
{
long v = 1;
for(int i = 2; i <= n; i++)
{
v = ((v * (i * 2) * (i * 2 - 1)) /
((i + 1) * (i)));
}
return v;
}
public static void main(String[] args)
{
int n = 4;
System.out.print("Number of Unique BST for " + n +
" nodes is " + numberOfBST(n) + "\n");
}
}
|
Python3
def numberOfBST(n):
v = 1
for i in range(2, n + 1):
v = ((v * (i * 2) * (i * 2 - 1)) / ((i + 1) * (i)))
return int(v)
n = 4
print("Number of Unique BST for", n, "nodes is", numberOfBST(n))
|
C#
using System;
class GFG {
static int numberOfBST(int n)
{
int v = 1;
for (int i = 2; i <= n; i++)
{
v = ((v * (i * 2) * (i * 2 - 1)) / ((i + 1) * (i)));
}
return v;
}
static void Main() {
int n = 4;
Console.Write("Number of Unique BST for " + n + " nodes is " + numberOfBST(n));
}
}
|
Javascript
<script>
function numberOfBST(n)
{
let v = 1;
for (let i = 2; i <= n; i++) {
v = ((v * (i * 2) * (i * 2 - 1)) / ((i + 1) * (i)));
}
return v;
}
let n = 4;
document.write("Number of Unique BST for " + n + " nodes is "
+ numberOfBST(n));
</script>
|
OutputNumber of Unique BST for 4 nodes is 14
Time Complexity: O(n)
Auxiliary Space: O(1).
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...