Total Derivative

Last Updated : 20 Mar, 2024

Total derivative of a function f at a point is an approximation near the point of function w.r.t. (with respect to) its arguments (variables). The total derivative never approximates the function with a single variable if two or more variables are present in the function.

Sometimes, the Total derivative is the same as the partial derivative or ordinary derivative of the function.

For Composite Function

In general composite, the function is nothing but a function of two or more dependent variables which depend upon any common variable t. Composite function values are obtained from both variables.

If u= f(x,y), where x and y are dependent variables at t, then we can also express u as a function of t. By substituting the value of x, y in f(x,y). Thus, we find the ordinary derivative which is called the total derivative of u.

Now, to find 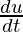$\frac{du}{dt}$ without actually substituting the value of x and y in f(x,y).

$\frac{du}{dt} =\frac{\partial u }{\partial x}. \frac{\partial x }{\partial t} + \frac{\partial u }{\partial y}. \frac{\partial y }{\partial t}$

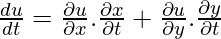
Similarly, If u = f(x,y,z) where x, y, and z are all functions of a variable t, then the chain rule is:

$\frac{du}{dt} =\frac{\partial u }{\partial x}. \frac{\partial x }{\partial t} + \frac{\partial u }{\partial y}. \frac{\partial y }{\partial t} + \frac{\partial u }{\partial z}. \frac{\partial z }{\partial t}$

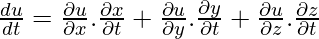
Question: Given, 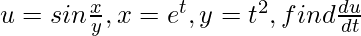$u = sin\frac{x}{y} , x = e^{t}, y= t^{2}, find \frac{du}{dt}$ as a function of t. Verify your result by direct substitution.

Solution:

We have, 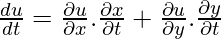$\frac{du}{dt} = \frac{\partial u }{\partial x}. \frac{\partial x }{\partial t} + \frac{\partial u }{\partial y}. \frac{\partial y }{\partial t}$

= $cos\frac{x}{y} . \frac{1}{y} . _e{t} + (cos\frac{x}{y}) (\frac{-x}{_y{2}^{ }}) .2t$

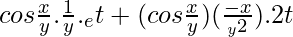
putting values of x and y in the above equations

= $cos\frac{_e{t}}{_t{2}} . \frac{_e{t}}{_t{2}} -2cos\frac{_e{t}}{_t{2}} . _e{t}._t{3}$

$\frac{du}{dt} = (t-\frac{2}{_t{3}})._e{t}.cos\frac{_e{t}}{_t{2}}$

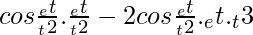
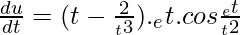
Question: Given, f(x,y) = e^xsiny , x = t³+1 and y = t⁴+1. Then df/dt at t = 1.

Solution:

Let f(x,y) =e^xsiny

$\frac{df}{dt} =\frac{\partial u }{\partial x}. \frac{\partial x }{\partial t} + \frac{\partial u }{\partial y}. \frac{\partial y }{\partial t}$

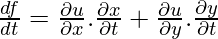
= e^xsiny.(3t²) + cosy .e^x .(4t³)

As we know , x= t³+1 and y= t⁴+1

x and y values at t =1, x=2 and y=2

$\frac{df}{dt} = (e^{2})(sin2)(12) + (cos2)(e^{2})(32)$

= (2.718)²(0.0349)(12) +(0.9994)(2.718)²(32)

= 238.97

For Implicit Function

The implicit function is a function whose variables are not completely independent variables. Let a function f(x,y) where x is independent variable but y is x dependent variable.

If f(x, y)= c ( constant )be an implicit function and relation between x and y exists which defines as a differentiable function of x.

Here, f(x,y) =constant

For implicit function let us consider, x an independent variable, and y is a function of x.

f(x,y) = c…….eq (1)

by definition of total differential coefficient.

Question: If u = x.log(xy) where x³ + y³+ 3xy = 1, find du/dx.

Solution:

We have x³ + y³+ 3xy = 1……….(1)

$\frac{du}{dx}=\frac{\partial u}{\partial x}.\frac{dy}{dx} +\frac{\partial u}{\partial y}.\frac{dy}{dx}$

= $(logxy +1) + \frac{x}{y}.\frac{dy}{dx} ..........(2)$

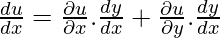
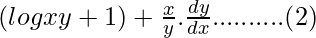
from eq……….(1)

$\frac {dy}{dx} = -\frac{\frac{∂f}{∂x}} { \frac{∂f}{∂y}}$

$\frac{dy}{dx} = -\frac {(3x^{2} + 3y)}{(3y^{2} + 3x)}$

$= -\frac{(x^{2} +y)}{(y^{2} +x)}t$

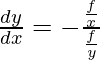
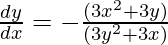
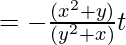
after putting value in eq (2)

$\frac{du}{dx} = (logxy +1) - (\frac{x}{y})\frac {(x^{2}+y)}{(y^{2}+x)} .$