Time-Space Trade-Off in Algorithms
Last Updated :
02 Nov, 2023
In this article, we will discuss Time-Space Trade-Off in Algorithms. A tradeoff is a situation where one thing increases and another thing decreases. It is a way to solve a problem in:
- Either in less time and by using more space, or
- In very little space by spending a long amount of time.
The best Algorithm is that which helps to solve a problem that requires less space in memory and also takes less time to generate the output. But in general, it is not always possible to achieve both of these conditions at the same time. The most common condition is an algorithm using a lookup table. This means that the answers to some questions for every possible value can be written down. One way of solving this problem is to write down the entire lookup table, which will let you find answers very quickly but will use a lot of space. Another way is to calculate the answers without writing down anything, which uses very little space, but might take a long time. Therefore, the more time-efficient algorithms you have, that would be less space-efficient.
Types of Space-Time Trade-off
- Compressed or Uncompressed data
- Re Rendering or Stored images
- Smaller code or loop unrolling
- Lookup tables or Recalculation
Compressed or Uncompressed data: A space-time trade-off can be applied to the problem of data storage. If data stored is uncompressed, it takes more space but less time. But if the data is stored compressed, it takes less space but more time to run the decompression algorithm. There are many instances where it is possible to directly work with compressed data. In that case of compressed bitmap indices, where it is faster to work with compression than without compression.
Re-Rendering or Stored images: In this case, storing only the source and rendering it as an image would take more space but less time i.e., storing an image in the cache is faster than re-rendering but requires more space in memory.
Smaller code or Loop Unrolling: Smaller code occupies less space in memory but it requires high computation time that is required for jumping back to the beginning of the loop at the end of each iteration. Loop unrolling can optimize execution speed at the cost of increased binary size. It occupies more space in memory but requires less computation time.
Lookup tables or Recalculation: In a lookup table, an implementation can include the entire table which reduces computing time but increases the amount of memory needed. It can recalculate i.e., compute table entries as needed, increasing computing time but reducing memory requirements.
For Example: In mathematical terms, the sequence Fn of the Fibonacci Numbers is defined by the recurrence relation:
Fn = Fn – 1 + Fn – 2,
where, F0 = 0 and F1 = 1.
A simple solution to find the Nth Fibonacci term using recursion from the above recurrence relation.
Below is the implementation using recursion:
C++
#include <iostream>
using namespace std;
int Fibonacci(int N)
{
if (N < 2)
return N;
return Fibonacci(N - 1) + Fibonacci(N - 2);
}
int main()
{
int N = 5;
cout << Fibonacci(N);
return 0;
}
|
Java
class GFG {
static int Fibonacci(int N)
{
if (N < 2)
return N;
return Fibonacci(N - 1) + Fibonacci(N - 2);
}
public static void main(String[] args)
{
int N = 5;
System.out.print(Fibonacci(N));
}
}
|
Python3
def Fibonacci(N:int):
if (N < 2):
return N
return Fibonacci(N - 1) + Fibonacci(N - 2)
if __name__ == '__main__':
N = 5
print(Fibonacci(N))
|
C#
using System;
class GFG
{
static int Fibonacci(int N)
{
if (N < 2)
return N;
return Fibonacci(N - 1) + Fibonacci(N - 2);
}
public static void Main(string[] args)
{
int N = 5;
Console.Write(Fibonacci(N));
}
}
|
Javascript
function Fibonacci(N)
{
if (N < 2)
return N;
return Fibonacci(N - 1) + Fibonacci(N - 2);
}
let N = 5;
console.log(Fibonacci(N));
|
Time Complexity: O(2N)
Auxiliary Space: O(1)
Explanation: The time complexity of the above implementation is exponential due to multiple calculations of the same subproblems again and again. The auxiliary space used is minimum. But our goal is to reduce the time complexity of the approach even it requires extra space. Below is the Optimized approach discussed.
Efficient Approach: To optimize the above approach, the idea is to use Dynamic Programming to reduce the complexity by memoization of the overlapping subproblems as shown in the below recursion tree:
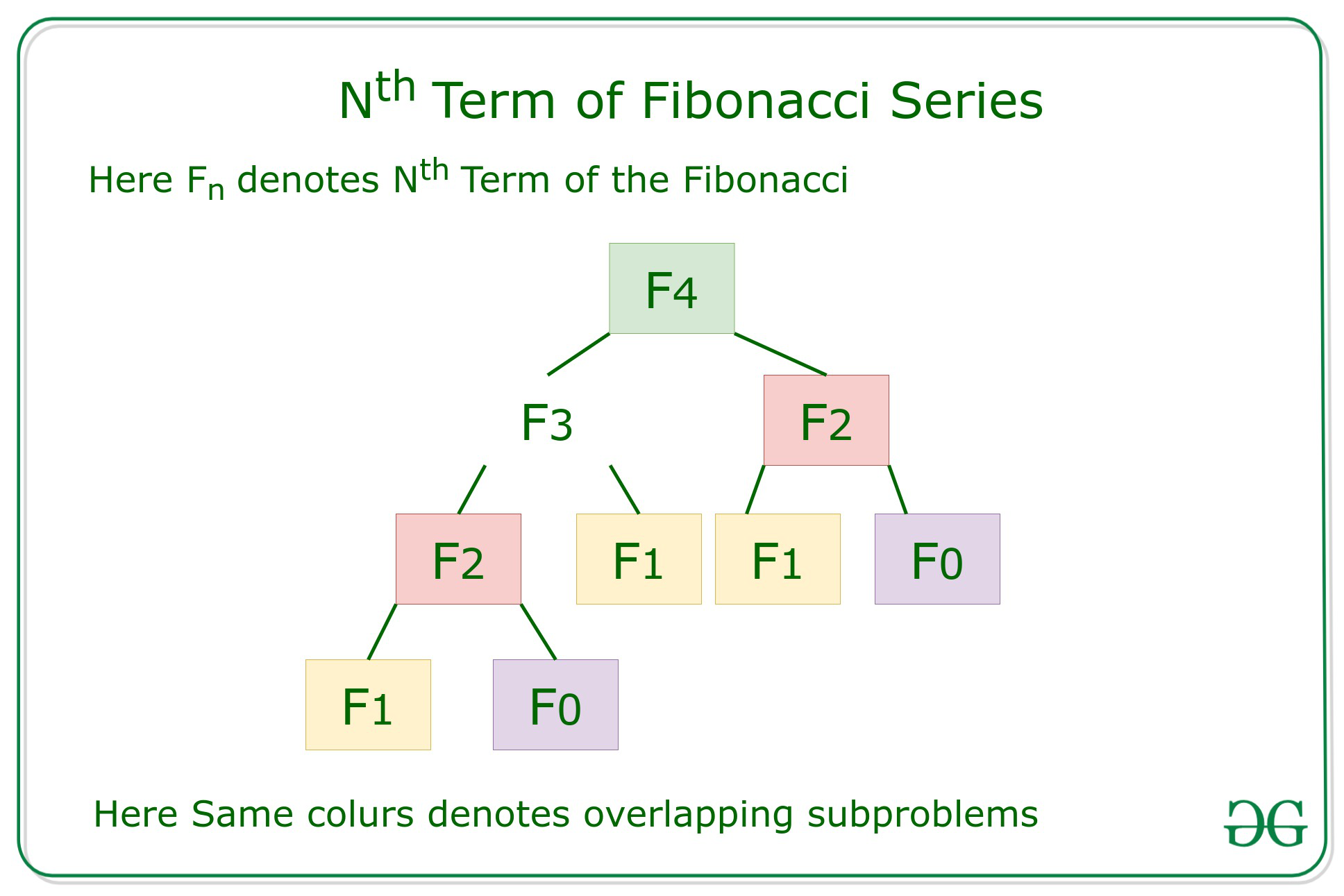
Below is the implementation of the above approach:
C++
#include <iostream>
using namespace std;
int Fibonacci(int N)
{
int f[N + 2];
int i;
f[0] = 0;
f[1] = 1;
for (i = 2; i <= N; i++) {
f[i] = f[i - 1] + f[i - 2];
}
return f[N];
}
int main()
{
int N = 5;
cout << Fibonacci(N);
return 0;
}
|
Java
import java.io.*;
class GFG {
static int Fibonacci(int N)
{
int[] f= new int[N + 2];
int i;
f[0] = 0;
f[1] = 1;
for (i = 2; i <= N; i++) {
f[i] = f[i - 1] + f[i - 2];
}
return f[N];
}
public static void main (String[] args)
{
int N = 5;
System.out.println(Fibonacci(N));
}
}
|
Python3
def Fibonacci(N):
f=[0]*(N + 2)
f[0] = 0
f[1] = 1
for i in range(2,N+1) :
f[i] = f[i - 1] + f[i - 2]
return f[N]
if __name__ == '__main__':
N = 5
print(Fibonacci(N))
|
C#
using System;
class GFG {
static int Fibonacci(int N)
{
int[] f= new int[N + 2];
int i;
f[0] = 0;
f[1] = 1;
for (i = 2; i <= N; i++) {
f[i] = f[i - 1] + f[i - 2];
}
return f[N];
}
public static void Main()
{
int N = 5;
Console.Write(Fibonacci(N));
}
}
|
Javascript
function fibonacci(N) {
const f = new Array(N + 2).fill(0);
f[0] = 0;
f[1] = 1;
for (let i = 2; i <= N; i++) {
f[i] = f[i - 1] + f[i - 2];
}
return f[N];
}
const N = 5;
console.log(fibonacci(N));
|
Time Complexity: O(N)
Auxiliary Space: O(N)
Explanation: The time complexity of the above implementation is linear by using an auxiliary space for storing the overlapping subproblems states so that it can be used further when required.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...