Tiling with Dominoes
Last Updated :
12 Dec, 2022
Given a 3 x n board, find the number of ways to fill it with 2 x 1 dominoes.
Example 1:
Following are all the 3 possible ways to fill up a 3 x 2 board.

Example 2:
Here is one possible way of filling a 3 x 8 board. You have to find all the possible ways to do so.

Examples :
Input : 2
Output : 3
Input : 8
Output : 153
Input : 12
Output : 2131
Defining Subproblems:
At any point while filling the board, there are three possible states that the last column can be in:

An = No. of ways to completely fill a 3 x n board. (We need to find this)
Bn = No. of ways to fill a 3 x n board with top corner in last column not filled.
Cn = No. of ways to fill a 3 x n board with bottom corner in last column not filled.
Note: The following states are impossible to reach:

Finding Recurrences
Note: Even though Bn and Cn are different states, they will be equal for same ‘n’. i.e Bn = Cn
Hence, we only need to calculate one of them.
Calculating An:

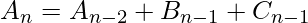
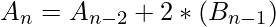
Calculating Bn:

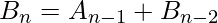
The final Recursive Relations are:
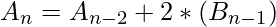
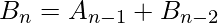
Base Cases:
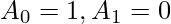
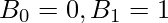
C++
#include <iostream>
using namespace std;
int countWays(int n)
{
int A[n + 1], B[n + 1];
A[0] = 1, A[1] = 0, B[0] = 0, B[1] = 1;
for (int i = 2; i <= n; i++) {
A[i] = A[i - 2] + 2 * B[i - 1];
B[i] = A[i - 1] + B[i - 2];
}
return A[n];
}
int main()
{
int n = 8;
cout << countWays(n);
return 0;
}
|
Java
import java.io.*;
class GFG {
static int countWays(int n)
{
int []A = new int[n+1];
int []B = new int[n+1];
A[0] = 1; A[1] = 0;
B[0] = 0; B[1] = 1;
for (int i = 2; i <= n; i++)
{
A[i] = A[i - 2] + 2 * B[i - 1];
B[i] = A[i - 1] + B[i - 2];
}
return A[n];
}
public static void main (String[] args)
{
int n = 8;
System.out.println(countWays(n));
}
}
|
Python 3
def countWays(n):
A = [0] * (n + 1)
B = [0] * (n + 1)
A[0] = 1
A[1] = 0
B[0] = 0
B[1] = 1
for i in range(2, n+1):
A[i] = A[i - 2] + 2 * B[i - 1]
B[i] = A[i - 1] + B[i - 2]
return A[n]
n = 8
print(countWays(n))
|
C#
using System;
class GFG {
static int countWays(int n)
{
int []A = new int[n+1];
int []B = new int[n+1];
A[0] = 1; A[1] = 0;
B[0] = 0; B[1] = 1;
for (int i = 2; i <= n; i++)
{
A[i] = A[i - 2] + 2 * B[i - 1];
B[i] = A[i - 1] + B[i - 2];
}
return A[n];
}
public static void Main ()
{
int n = 8;
Console.WriteLine(countWays(n));
}
}
|
Javascript
<script>
function countWays(n)
{
let A = new Array(n+1);
let B = new Array(n+1);
A[0] = 1; A[1] = 0;
B[0] = 0; B[1] = 1;
for (let i = 2; i <= n; i++)
{
A[i] = A[i - 2] + 2 * B[i - 1];
B[i] = A[i - 1] + B[i - 2];
}
return A[n];
}
let n = 8;
document.write(countWays(n));
</script>
|
PHP
<?php
function countWays($n)
{
$A = array();
$B = array();
$A[0] = 1; $A[1] = 0;
$B[0] = 0; $B[1] = 1;
for ( $i = 2; $i <= $n; $i++)
{
$A[$i] = $A[$i - 2] + 2 *
$B[$i - 1];
$B[$i] = $A[$i - 1] +
$B[$i - 2];
}
return $A[$n];
}
$n = 8;
echo countWays($n);
?>
|
Time Complexity: O(N)
Auxiliary Space: O(N)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...