L-graphs and what they represent in TOC
Last Updated :
07 Feb, 2023
Prerequisite – Finite automata introduction All programming languages can be represented as a finite automata. C, Paskal, Haskell, C++, all of them have a specific structure, grammar, that can be represented by a simple graph. Most of the graphs are NFA’s or DFA’s. But NFA’s and DFA’s determine the simplest possible language group: group of regular languages [Chomsky’s hierarchy]. This leaves us with a question: what about all other types of languages? One of the answers is Turing machine, but a Turing machine is hard to visualize. This is why in this article I will tell you about a type of finite automata called an L-graph. In order to understand how L-graphs work we need to know what type of languages L-graphs determine. To put it simply, L-graphs represent context-sensitive type of languages [and every other type that the context-sensitive group contains]. If you don’t know what “context-sensitive” means, let me show you an example of a language that can be represented by an L-graph and not by any easier type of finite automata. This language is 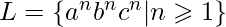 . Corresponding L-graph looks like this:
. Corresponding L-graph looks like this: 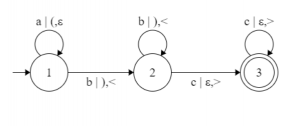 As you can see the brackets after the symbol ‘|’ control the numbers of symbols that come after the symbols ‘a’. This leads us to the two features that all L-graphs possess: all L-graphs have up to two independent from each other and from input symbols bracket groups, both bracket groups have to be right [string from a Dyck language] in order for the string of input symbols to be accepted by the given L-graph. You can see that an L-graph is just a version of finite automata with an added couple of bracket groups. To help you get an understanding of why the languages determined by L-graphs are context-sensitive, check what strings the L-graph shown above has to accept.
As you can see the brackets after the symbol ‘|’ control the numbers of symbols that come after the symbols ‘a’. This leads us to the two features that all L-graphs possess: all L-graphs have up to two independent from each other and from input symbols bracket groups, both bracket groups have to be right [string from a Dyck language] in order for the string of input symbols to be accepted by the given L-graph. You can see that an L-graph is just a version of finite automata with an added couple of bracket groups. To help you get an understanding of why the languages determined by L-graphs are context-sensitive, check what strings the L-graph shown above has to accept. 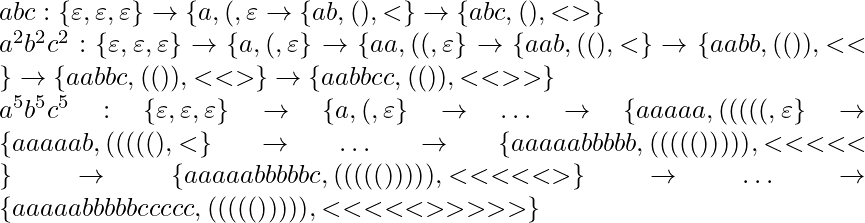 To conclude, I would like to add three other definitions that I’ll be using in the future. These definitions are very important for the hypothesis [and its future proof or disproof]. Refer – Hypothesis (language regularity) and algorithm (L-graph to NFA) We will call a path in the L-graph neutral, if both bracket strings are right. If a neutral path T can be represented like this, T =
To conclude, I would like to add three other definitions that I’ll be using in the future. These definitions are very important for the hypothesis [and its future proof or disproof]. Refer – Hypothesis (language regularity) and algorithm (L-graph to NFA) We will call a path in the L-graph neutral, if both bracket strings are right. If a neutral path T can be represented like this, T = 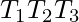 , where
, where 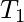 and
and 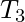 are cycles and
are cycles and 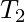 is a neutral path (
is a neutral path (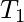 ,
, 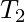 or
or 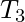 can be empty), T is called a nest. We can also say that the three (
can be empty), T is called a nest. We can also say that the three (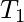 ,
, 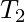 ,
, 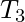 ) is a nest or that
) is a nest or that 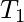 and
and 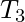 form a nest in the path T. (
form a nest in the path T. (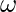 , d)-core in an L-graph G, defined as Core(G,
, d)-core in an L-graph G, defined as Core(G, 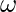 , d), is a set of (
, d), is a set of (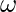 , d)-canons. (
, d)-canons. (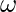 , d)-canon, where
, d)-canon, where 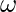 and d are positive whole numbers, is a path that contains at most m,
and d are positive whole numbers, is a path that contains at most m,  , neutral cycles and at most k, k
, neutral cycles and at most k, k 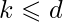 d, nests that can be represented this way:
d, nests that can be represented this way: 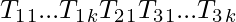 is part of the path T,
is part of the path T, 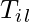 , i = 1 or 3,
, i = 1 or 3, 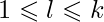 , are cycles, every path
, are cycles, every path 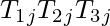 is a nest, where
is a nest, where 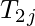 =
= 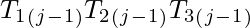 ,
,  . The last definition is about a context free L-graph. An L-graph G is called context free if G has only one bracket group (all rules in the L-graph have only one look of these two: [‘symbol’ | ‘bracket’, ?] or [‘symbol’ | ?, ‘bracket’]). [Definition of a Dyck language.
. The last definition is about a context free L-graph. An L-graph G is called context free if G has only one bracket group (all rules in the L-graph have only one look of these two: [‘symbol’ | ‘bracket’, ?] or [‘symbol’ | ?, ‘bracket’]). [Definition of a Dyck language.  and
and 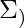 are disjoint alphabets. There exists a bijection (function that for every element from the 1st set matches one and only one element from the 2nd set)
are disjoint alphabets. There exists a bijection (function that for every element from the 1st set matches one and only one element from the 2nd set) 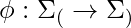 . Then the language defined by the grammar
. Then the language defined by the grammar 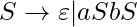 ,
, 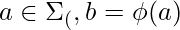 , we will call a Dyck language.]
, we will call a Dyck language.]
Example
A real-life example of using L-graphs could be in the context of a company’s organizational structure.
Imagine a company with different departments (sales, marketing, finance, HR, etc.) and each department has different sub-departments. We can represent this organizational structure as a graph where each vertex represents a department and the edges represent the relationships between them (i.e, which department is a sub-department of another).
Now, let’s say we want to represent the relationships between the managers of each department. We can create an L-graph, where each vertex represents a manager and the edges represent the relationships between them (i.e, which manager is the supervisor of another).
In this scenario, the original graph represents the overall structure of the company, while the L-graph represents the relationship between the managers. This can be useful for understanding the chain of command and decision-making processes within the company.
It’s worth to mention that this is a simple example and in real life scenarios L-graphs can be used to represent much more complex systems and relations and these graphs are used in various fields such as computer science, mathematics, physics, and engineering.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...